Confidence Interval: Are you Interpreting Correctly? | by Vivekananda Das | Jul, 2022
An intuitive explanation
In my previous article, I discussed why you should prefer reporting 95% confidence interval over p-value, especially when you are explaining the findings of your study to non-statistician readers/audiences. In this article, I continue the discussion further and try to provide a bit more clarity.
Regarding the “correct” interpretation of the confidence interval, one of my readers asked a great question:
As a student, I had the same question for a long time. Indeed, for many of us, these are unintuitive concepts.
We have the impression that statistics is about explaining data through cool graphs, estimating magical models, etc. And all these statements are correct. However, after four years of education, my understanding is that, at its core, statistics is about reducing the complexity of a world full of unknowns with the end goal of making some sophisticated guesses about what we don’t know based on what we know through a systematic process. Unfortunately, most humans inherently prefer certainty over uncertainty because the latter makes us feel uncomfortable. My hypothesis is that our desire for “certainty” is one of the key reasons why many of us struggle to grasp the fundamentals of statistics.
Okay! Let’s focus on my reader’s concern now. Why do these two statements imply different things? 🤔
Statement 1: We are 95% confident that the bowl contains the apple
Statement 2: We are 95% confident that the apple is in the bowl
These two statements refer to two different games of uncertainties.
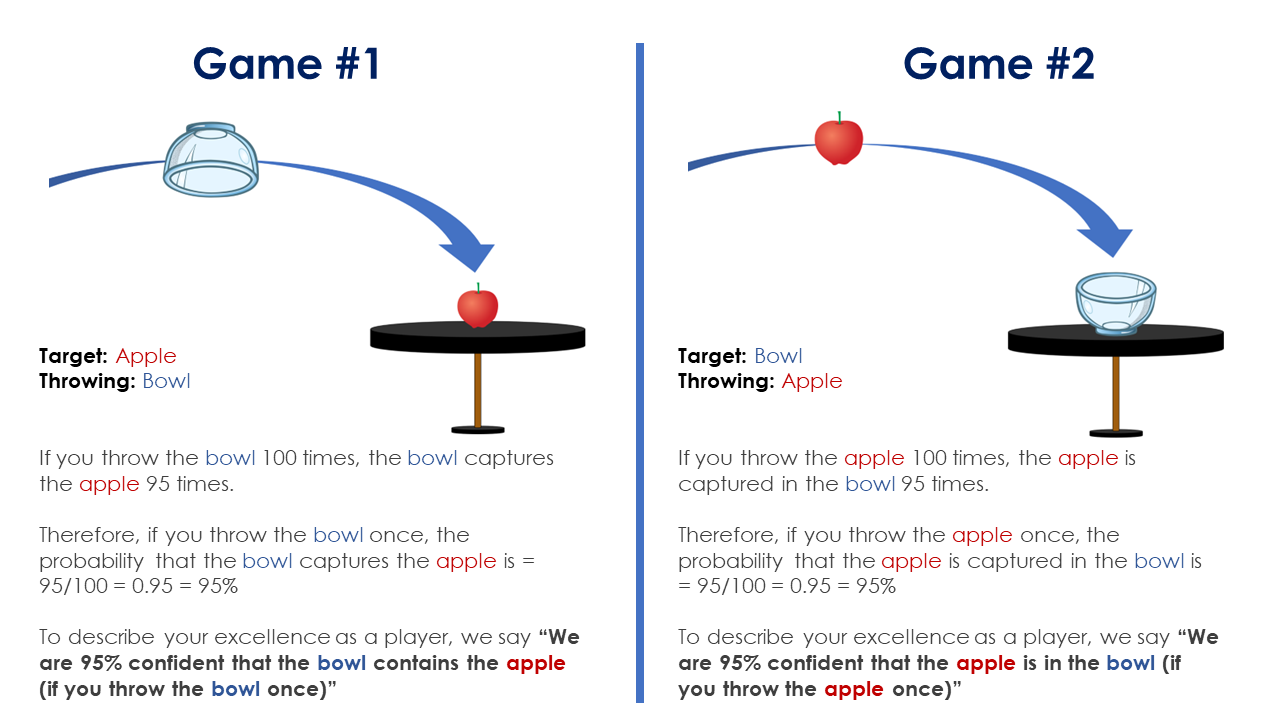
There is an apple sitting still on a table. The apple is the target and it exists at a fixed location. There is no uncertainty regarding the apple. It exists where it exists.
As a player, you get a bowl to throw at the apple. The goal is that the bowl captures the apple (upside down).
You are quite good at the game.
If you throw the bowl 100 times, the bowl captures the apple 95 times.
Therefore, if you throw the bowl once, the probability that the bowl captures the apple is = 95/100 = 0.95 = 95%
To describe your excellence as a player, we say “We are 95% confident that the bowl contains the apple (if you throw the bowl once)”.
There is a bowl sitting still on a table. The bowl is the target and it exists at a fixed location. There is no uncertainty regarding the bowl. It exists where it exists.
As a player, you get an apple to throw at the bowl. The goal is that the apple is captured in the bowl.
You are quite good at the game.
If you throw the apple 100 times, the apple is captured in the bowl 95 times.
Therefore, if you throw the apple once, the probability that the apple is captured in the bowl is = 95/100 = 0.95 = 95%
To describe your excellence as a player, we say “We are 95% confident that the apple is in the bowl (if you throw the bowl once)”.
(1) The target parameter has no uncertainty. It exists at a fixed place (at least we assume it does) at any given point in time.
(2) The thing which we are throwing at the target parameter has uncertainty regarding whether it captures the fixed target or not🎯. Therefore, the statement of probability should be with respect to whether the thrown thing captures the fixed target or not.
At a hypothetical university, the average weight (body mass to be more precise) of students is 130 lbs. It is a fixed number (at any given point in time) but it is unknown to you. As a researcher, you are trying to estimate the population average weight.
There are 10,000 students at the university and it is not possible for you to weigh each individual student and record their weight. You get a list of all the students and randomly select 100 of them.
They all agree to let you measure their weight. And you collect the information. The sample average weight is 125 lbs.
You realize that this is just one sample — out of an infinite number of samples that could have been drawn — from the target population. If you draw another sample from the same population, then the sample average weight could be 132 lbs, or 120 lbs, or 142 lbs, or some other value. You want to reduce this uncertainty by constructing an interval of possible numbers.
Let’s assume, for the one sample you selected, the 95% confidence interval is = [115 lbs, 135 lbs].
You say “ I am 95% confident that *this interval* captures the true population average weight”.
This is not the same as saying “I am 95% confident that *the true population average weight* is captured in the interval.”
The true population average is your target parameter which exists somewhere in the universe and you assume it is a fixed number at any given point in time. Because it is not changing, the statement on uncertainty is not with respect to it.
The confidence intervals, which you can possibly construct, have uncertainties associated with them. If you draw 100 samples from the same population → you get 100 different confidence intervals → 95 of them are expected to capture the true population parameter. You are, as if, throwing confidence intervals at the fixed population parameter.
The above narrative implies if you draw only one sample, the probability that the confidence interval captures the true population parameter (i.e., the fixed target) is 95%.
Without delving too deep into philosophy, in colloquial English,
The bowl contains the apple == The apple is in the bowl
The two statements imply the same thing because we are in the land of certainty. When we believe that we know something for sure, we do not make any probabilistic statements. (please don’t ask: do we know anything for sure? 🙏)
However, when we are in the land of “some” uncertainty, in statistical English,
We are 95% confident that the bowl contains the apple =/= We are 95% confident that the apple is in the bowl
I hope this helps. Again, I appreciate your great comments on my articles. I hope we continue this discussion and help each other make sense of the complex world with a bit more clarity.
Meanwhile, if you would like to read some of my previous posts on how to attempt to know the unknown, here are some suggestions:
An intuitive explanation
In my previous article, I discussed why you should prefer reporting 95% confidence interval over p-value, especially when you are explaining the findings of your study to non-statistician readers/audiences. In this article, I continue the discussion further and try to provide a bit more clarity.
Regarding the “correct” interpretation of the confidence interval, one of my readers asked a great question:
As a student, I had the same question for a long time. Indeed, for many of us, these are unintuitive concepts.
We have the impression that statistics is about explaining data through cool graphs, estimating magical models, etc. And all these statements are correct. However, after four years of education, my understanding is that, at its core, statistics is about reducing the complexity of a world full of unknowns with the end goal of making some sophisticated guesses about what we don’t know based on what we know through a systematic process. Unfortunately, most humans inherently prefer certainty over uncertainty because the latter makes us feel uncomfortable. My hypothesis is that our desire for “certainty” is one of the key reasons why many of us struggle to grasp the fundamentals of statistics.
Okay! Let’s focus on my reader’s concern now. Why do these two statements imply different things? 🤔
Statement 1: We are 95% confident that the bowl contains the apple
Statement 2: We are 95% confident that the apple is in the bowl
These two statements refer to two different games of uncertainties.
There is an apple sitting still on a table. The apple is the target and it exists at a fixed location. There is no uncertainty regarding the apple. It exists where it exists.
As a player, you get a bowl to throw at the apple. The goal is that the bowl captures the apple (upside down).
You are quite good at the game.
If you throw the bowl 100 times, the bowl captures the apple 95 times.
Therefore, if you throw the bowl once, the probability that the bowl captures the apple is = 95/100 = 0.95 = 95%
To describe your excellence as a player, we say “We are 95% confident that the bowl contains the apple (if you throw the bowl once)”.
There is a bowl sitting still on a table. The bowl is the target and it exists at a fixed location. There is no uncertainty regarding the bowl. It exists where it exists.
As a player, you get an apple to throw at the bowl. The goal is that the apple is captured in the bowl.
You are quite good at the game.
If you throw the apple 100 times, the apple is captured in the bowl 95 times.
Therefore, if you throw the apple once, the probability that the apple is captured in the bowl is = 95/100 = 0.95 = 95%
To describe your excellence as a player, we say “We are 95% confident that the apple is in the bowl (if you throw the bowl once)”.
(1) The target parameter has no uncertainty. It exists at a fixed place (at least we assume it does) at any given point in time.
(2) The thing which we are throwing at the target parameter has uncertainty regarding whether it captures the fixed target or not🎯. Therefore, the statement of probability should be with respect to whether the thrown thing captures the fixed target or not.
At a hypothetical university, the average weight (body mass to be more precise) of students is 130 lbs. It is a fixed number (at any given point in time) but it is unknown to you. As a researcher, you are trying to estimate the population average weight.
There are 10,000 students at the university and it is not possible for you to weigh each individual student and record their weight. You get a list of all the students and randomly select 100 of them.
They all agree to let you measure their weight. And you collect the information. The sample average weight is 125 lbs.
You realize that this is just one sample — out of an infinite number of samples that could have been drawn — from the target population. If you draw another sample from the same population, then the sample average weight could be 132 lbs, or 120 lbs, or 142 lbs, or some other value. You want to reduce this uncertainty by constructing an interval of possible numbers.
Let’s assume, for the one sample you selected, the 95% confidence interval is = [115 lbs, 135 lbs].
You say “ I am 95% confident that *this interval* captures the true population average weight”.
This is not the same as saying “I am 95% confident that *the true population average weight* is captured in the interval.”
The true population average is your target parameter which exists somewhere in the universe and you assume it is a fixed number at any given point in time. Because it is not changing, the statement on uncertainty is not with respect to it.
The confidence intervals, which you can possibly construct, have uncertainties associated with them. If you draw 100 samples from the same population → you get 100 different confidence intervals → 95 of them are expected to capture the true population parameter. You are, as if, throwing confidence intervals at the fixed population parameter.
The above narrative implies if you draw only one sample, the probability that the confidence interval captures the true population parameter (i.e., the fixed target) is 95%.
Without delving too deep into philosophy, in colloquial English,
The bowl contains the apple == The apple is in the bowl
The two statements imply the same thing because we are in the land of certainty. When we believe that we know something for sure, we do not make any probabilistic statements. (please don’t ask: do we know anything for sure? 🙏)
However, when we are in the land of “some” uncertainty, in statistical English,
We are 95% confident that the bowl contains the apple =/= We are 95% confident that the apple is in the bowl
I hope this helps. Again, I appreciate your great comments on my articles. I hope we continue this discussion and help each other make sense of the complex world with a bit more clarity.
Meanwhile, if you would like to read some of my previous posts on how to attempt to know the unknown, here are some suggestions:
Denial of responsibility! Techno Blender is an automatic aggregator of the all world’s media. In each content, the hyperlink to the primary source is specified. All trademarks belong to their rightful owners, all materials to their authors. If you are the owner of the content and do not want us to publish your materials, please contact us by email – [email protected]. The content will be deleted within 24 hours.