Optimizing TV Programs Scheduling Using Genetic Algorithms in Python

By Jessie Hobb On Jul 26, 2023

A hands-on tutorial explaining how to optimize TV program scheduling using Genetic Algorithm in Python

Photo by Glenn Carstens-Peters on Unsplash

It’s been a long time since I wrote a new post on Medium. For two years, I have been researching what improvements can be made in the traditional media sector through machine learning and deep learning. One of these research areas is optimization techniques. As in every industry, optimization is essential in media. Thus, in this article, I want to share TV program planning by integrating it into an evolution algorithm, a Genetic Algorithm. Remember, this is just a straightforward implementation. Real life goes far beyond this simplicity.

WHAT IS OPTIMIZATION, AND WHY DO WE NEED THIS?

What is optimization? I want to start with this question. Optimization is searching for values that minimize or maximize a given objective function. What about the objective function? The objective function is a mathematical representation of the performance measure we are trying to maximize or minimize. If the problem is a minimization problem, we can call it a cost function; if it is a maximization problem, we can call it a fitness function.

Let’s enrich this explanation with an example. Stop for a minute and imagine that you own a restaurant. We aim to maximize its profits by modifying the menu (by menu, I mean the dishes on the menu). The first method that comes to mind is to use cheaper ingredients. You can make more profit by reducing the quality of the ingredients used. But that’s not how things work in real life. When you lower product quality, customers reduce their demand for dishes made with lower-quality ingredients. Therefore, it is not possible to reach the desired goal.

As you can figure out, it is an optimization problem for the restaurant owner to create a menu to maximize their profit. For instance, the restaurant owner can analyze which plates are sold at what times and outline a road map. Optimization techniques will allow the restaurant owner to make a data-driven decision and achieve the best possible outcomes.

Now imagine that you work as a program planner for a television station. Remember that your competitors are strong, but you still have programs that can compete. The main problem that needs to be decided is which program should be broadcast at what time. It looks easy. A pen and some paper are enough. Is it really so?

Even though television program planning seems uncomplicated, it becomes very complex with the involvement of various factors. Here are some of these:

Viewer preferences: What TV content genres do viewers prefer?

Time slots: What kind of programs do the viewers prefer in what periods?

Lead-in and Lead-out programs: Some programs transfer the audience they collect during the broadcasting period to the next program.

Program preferences of competitor channels: What program are competing channels broadcasting at what time?

Holidays, special occasions, and seasonal trends: How are viewer preferences changing? Are there any existing trends?

Fresh and old content: Are the broadcast programs fresh? Or is it a rerun?

Storylines and Cliffhangers: Does the program have a storyline? Or cliffhanger?

These are just a few factors. You may have noticed that dozens of factors affect TV program planning. Therefore, optimizing algorithms to solve such problems would be suitable.

WHAT ARE THE EVALUATION AND GENETIC ALGORITHMS?

I will briefly explain evaluation and genetic algorithms in this part. Evolutionary Algorithms (EAs) are optimization techniques that can solve many challenging optimization problems without requiring specific knowledge about the problem structure; in other words, they are problem-independent. Evolutionary Algorithms (EAs) can handle linear and nonlinear objective functions without requiring information about the problem’s structure.
On the other hand, the genetic algorithm belongs to the family of search algorithms and uses the principles of evolution. By implementing reproduction and natural selection processes, it can produce solutions of high quality. The genetic algorithm is a highly effective technique for solving optimization problems.

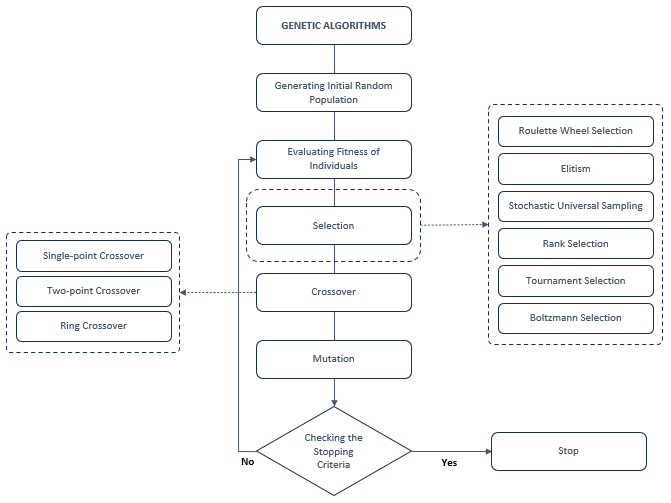
You can see a simple GA flowchart below. Our first step is to create an initial population. The initial population contains randomly selected chromosomes (more clearly, the initial population is a set of chromosomes). After the population is created, a fitness function value is calculated for each individual. Genetic algorithms use a chromosome to represent each individual. The fitness value of each individual is independent of the others. In this way, multiple calculations can be made at the same time. After the fitness values are calculated, three different phases of the GA come into play — selection, crossover, and mutation. The selection phase is responsible for selecting chromosomes from the population. The aim is to create better generations. The crossover process is responsible for developing new offspring from selected individuals. This process is usually done by taking two selected individuals at a time and interchanging parts of their chromosomes to create two new chromosomes representing the offspring. Finally, the operator changes one or more genes in the mutation phase. The probability of this change is very low. The most important feature of the mutation phase is to prevent the system from getting stuck in the local minima.

Genetic algorithms flow chart (Eser Saygın)

IMPLEMENTATION

I just gave simple information about the genetic algorithm. Now I will explain the genetic algorithm step by step using Python. Our problem, as seen in the title, is which program will be broadcast at what time. First of all, there is an important point that I should emphasize. The problem we will implement in a moment is a simple example. As I mentioned, many factors affect the problem’s implementation in real life. For this reason, the problem identification phase is the most time-consuming part.

STEPS

First, we start by defining our dataset. As I mentioned earlier, the set below is a simple example. The dataset shows the ratings of various programs over 18 hours (06:00–24:00). In real life, it is necessary to broadcast in each time slot to measure the rating score of a program in different time slots.

# Sample rating programs dataset for each time slot.
ratings = {
    'news': [0.1, 0.1, 0.4, 0.3, 0.5, 0.4, 0.3, 0.2, 0.1, 0.2, 0.3, 0.5, 0.5, 0.4, 0.3, 0.2, 0.1, 0.2],
    'live_soccer': [0.0, 0.0, 0.0, 0.2, 0.1, 0.3, 0.2, 0.1, 0.4, 0.3, 0.4, 0.5, 0.4, 0.6, 0.4, 0.3, 0.4, 0.3],
    'movie_a': [0.1, 0.1, 0.2, 0.4, 0.3, 0.2, 0.1, 0.2, 0.3, 0.4, 0.5, 0.4, 0.3, 0.4, 0.3, 0.5, 0.3, 0.4],
    'movie_b': [0.2, 0.1, 0.1, 0.3, 0.2, 0.1, 0.2, 0.3, 0.4, 0.5, 0.4, 0.3, 0.4, 0.5, 0.4, 0.3, 0.4, 0.5],
    'reality_show': [0.3, 0.4, 0.3, 0.4, 0.4, 0.5, 0.3, 0.4, 0.5, 0.4, 0.3, 0.2, 0.1, 0.2, 0.3, 0.2, 0.2, 0.3],
    'tv_series_a': [0.2, 0.3, 0.2, 0.1, 0.1, 0.2, 0.2, 0.4, 0.4, 0.3, 0.3, 0.3, 0.5, 0.6, 0.4, 0.5, 0.4, 0.3],
    'tv_series_b': [0.1, 0.2, 0.3, 0.3, 0.2, 0.3, 0.3, 0.1, 0.4, 0.3, 0.4, 0.3, 0.5, 0.3, 0.4, 0.6, 0.4, 0.3],
    'music_program': [0.3, 0.3, 0.3, 0.2, 0.2, 0.1, 0.2, 0.4, 0.3, 0.3, 0.3, 0.3, 0.2, 0.3, 0.2, 0.3, 0.5, 0.3],
    'documentary': [0.3, 0.3, 0.4, 0.3, 0.2, 0.2, 0.3, 0.4, 0.4, 0.3, 0.2, 0.2, 0.2, 0.1, 0.1, 0.3, 0.3, 0.2],
    'Boxing': [0.4, 0.3, 0.3, 0.2, 0.2, 0.1, 0.1, 0.1, 0.1, 0.3, 0.3, 0.3, 0.2, 0.3, 0.4, 0.3, 0.4, 0.6]
}

Below, you can see the other variables. These variables are hyperparameters to be used in Genetic Algorithms. I’ve also created two different lists to use later.

GEN = 100
POP = 50
CO_R = 0.8
MUT_R = 0.2
EL_S = 2

all_programs = list(ratings.keys()) # all programs
all_time_slots = list(range(6, 24)) # time slots

As we mentioned in our article, our first job will be to initialize the population. You can find the function I created for this purpose below. As you can see, the function needs two input lists: a program list and a time slot list. We have already defined these lists above. The function generates all the potential schedules.

def initialize_pop(programs, time_slots):
    if not programs:
        return [[]]

    all_schedules = []
    for i in range(len(programs)):
        for schedule in initialize_pop(programs[:i] + programs[i + 1:], time_slots):
            all_schedules.append([programs[i]] + schedule)

    return all_schedules

Next, we will define our fitness function. The fitness function is responsible for measuring the quality of each schedule. It takes the schedule as input and returns the total rating score. (The list we call a schedule is a broadcast schedule consisting of TV programs.)

def fitness_function(schedule):
    total_rating = 0
    for time_slot, program in enumerate(schedule):
        total_rating += ratings[program][time_slot]
    return total_rating

After defining the fitness function, we can move on to the selection phase. The selection phase aims to find the most optimal schedule. For this, we can use the following function that we created. The function checks the fitness value of each schedule and chooses the one with the highest value.

def finding_best_schedule(all_schedules):
    best_schedule = []
    max_ratings = 0

    for schedule in all_schedules:
        total_ratings = fitness_function(schedule)
        if total_ratings > max_ratings:
            max_ratings = total_ratings
            best_schedule = schedule

    return best_schedule

The selection phase is followed by the crossover phase. In the crossover phase, two-parent solutions are combined with the help of GA to form a new offspring. In the TV schedule problem, this process changes the programs (genes) found in two solutions. This process creates various combinations of TV programs. You can see the crossover function below.

def crossover(schedule1, schedule2):
    crossover_point = random.randint(1, len(schedule1) - 2)
    child1 = schedule1[:crossover_point] + schedule2[crossover_point:]
    child2 = schedule2[:crossover_point] + schedule1[crossover_point:]
    return child1, child2

The final phase is the mutation phase. As we mentioned before, in the mutation phase, new offspring are formed by changing the genetic material of the chromosomes. In the TV program optimization problem, we can think of it as changing the program randomly. Remember, the probability of mutation is very low. Also, you can assign this possibility as a hyperparameter.

def mutate(schedule):
    mutation_point = random.randint(0, len(schedule) - 1)
    new_program = random.choice(all_programs)
    schedule[mutation_point] = new_program
    return schedule

Now that we have defined all our functions, we can run the fitness function.

# calling the fitness func.
def evaluate_fitness(schedule):
    return fitness_function(schedule)

The data we need for our genetic algorithm is ready. Now we can define the algorithm. This algorithm will use the initial_schedule, generations, population_size, crossover_rate, mutation_rate, and elitism_size. We have described these before. Since they are hyperparameters, we can modify them but don’t need to. The function begins by creating the initial population with the provided initial schedule and then adding random schedules. After that, it runs a loop for the specified number of generations and generates a new population for each generation using selection, crossover, and mutation operations. Elitism helps to preserve the most successful individuals from the previous generation based on their fitness scores. Once the population has been updated, it becomes the current population for the next generation. After that, the function returns the best schedule from the previous generation.

def genetic_algorithm(initial_schedule, generations=GEN, population_size=POP, crossover_rate=CO_R, mutation_rate=MUT_R, elitism_size=EL_S):
    
    population = [initial_schedule]

    for _ in range(population_size - 1):
        random_schedule = initial_schedule.copy()
        random.shuffle(random_schedule)
        population.append(random_schedule)

    for generation in range(generations):
        new_population = []

        # Elitism
        population.sort(key=lambda schedule: fitness_function(schedule), reverse=True)
        new_population.extend(population[:elitism_size])

        while len(new_population) < population_size:
            parent1, parent2 = random.choices(population, k=2)
            if random.random() < crossover_rate:
                child1, child2 = crossover(parent1, parent2)
            else:
                child1, child2 = parent1.copy(), parent2.copy()

            if random.random() < mutation_rate:
                child1 = mutate(child1)
            if random.random() < mutation_rate:
                child2 = mutate(child2)

            new_population.extend([child1, child2])

        population = new_population

    return population[0]

Now we are ready to get the results.

initial_best_schedule = finding_best_schedule(all_possible_schedules)

rem_t_slots = len(all_time_slots) - len(initial_best_schedule)
genetic_schedule = genetic_algorithm(initial_best_schedule, generations=GEN, population_size=POP, elitism_size=EL_S)

final_schedule = initial_best_schedule + genetic_schedule[:rem_t_slots]

print("\nFinal Optimal Schedule:")
for time_slot, program in enumerate(final_schedule):
    print(f"Time Slot {all_time_slots[time_slot]:02d}:00 - Program {program}")

print("Total Ratings:", fitness_function(final_schedule))

After the genetic algorithm has run, we combine the initial best and genetic schedules to create the final optimal schedule. Finally, we print the optimal schedule with the assigned programs, showing the time slot, the corresponding program, and the total ratings achieved in the final optimal schedule.

CONCLUSION

Program planning is crucial for television channels in the traditional media sector, where competition is high. In this case, we have shown how to improve TV program scheduling by utilizing a genetic algorithm, a powerful tool that can help maximize viewer ratings. Consider using a genetic algorithm to optimize a scheduling problem, such as TV program scheduling. With its powerful capabilities, it can help you create a schedule that maximizes viewer engagement and ratings.

In my upcoming articles, I plan to explore various Genetic algorithms like Competitive Co-Evolutionary (CCQGA) and Quantum (QGA). I may also include additional content in between.

Thank you for taking the time to read this article. If you’d like to connect with me, feel free to add me on LinkedIn.

https://www.linkedin.com/in/esersaygin/

SOURCES

Hands-On Genetic Algorithms with Python: Applying genetic algorithms to solve real-world deep learning and artificial intelligence problems by Eyal Wirsansky (Author)

Applied Evolutionary Algorithms for Engineers Using Python 1st Edition
by Leonardo Azevedo Scardua (Author)

FULL CODE

import random

##################################### DEFINING PARAMETERS AND DATASET ################################################################
# Sample rating programs dataset for each time slot.
ratings = {
    'news': [0.1, 0.1, 0.4, 0.3, 0.5, 0.4, 0.3, 0.2, 0.1, 0.2, 0.3, 0.5, 0.5, 0.4, 0.3, 0.2, 0.1, 0.2],
    'live_soccer': [0.0, 0.0, 0.0, 0.2, 0.1, 0.3, 0.2, 0.1, 0.4, 0.3, 0.4, 0.5, 0.4, 0.6, 0.4, 0.3, 0.4, 0.3],
    'movie_a': [0.1, 0.1, 0.2, 0.4, 0.3, 0.2, 0.1, 0.2, 0.3, 0.4, 0.5, 0.4, 0.3, 0.4, 0.3, 0.5, 0.3, 0.4],
    'movie_b': [0.2, 0.1, 0.1, 0.3, 0.2, 0.1, 0.2, 0.3, 0.4, 0.5, 0.4, 0.3, 0.4, 0.5, 0.4, 0.3, 0.4, 0.5],
    'reality_show': [0.3, 0.4, 0.3, 0.4, 0.4, 0.5, 0.3, 0.4, 0.5, 0.4, 0.3, 0.2, 0.1, 0.2, 0.3, 0.2, 0.2, 0.3],
    'tv_series_a': [0.2, 0.3, 0.2, 0.1, 0.1, 0.2, 0.2, 0.4, 0.4, 0.3, 0.3, 0.3, 0.5, 0.6, 0.4, 0.5, 0.4, 0.3],
    'tv_series_b': [0.1, 0.2, 0.3, 0.3, 0.2, 0.3, 0.3, 0.1, 0.4, 0.3, 0.4, 0.3, 0.5, 0.3, 0.4, 0.6, 0.4, 0.3],
    'music_program': [0.3, 0.3, 0.3, 0.2, 0.2, 0.1, 0.2, 0.4, 0.3, 0.3, 0.3, 0.3, 0.2, 0.3, 0.2, 0.3, 0.5, 0.3],
    'documentary': [0.3, 0.3, 0.4, 0.3, 0.2, 0.2, 0.3, 0.4, 0.4, 0.3, 0.2, 0.2, 0.2, 0.1, 0.1, 0.3, 0.3, 0.2],
    'Boxing': [0.4, 0.3, 0.3, 0.2, 0.2, 0.1, 0.1, 0.1, 0.1, 0.3, 0.3, 0.3, 0.2, 0.3, 0.4, 0.3, 0.4, 0.6]
}

GEN = 100
POP = 50
CO_R = 0.8
MUT_R = 0.2
EL_S = 2

all_programs = list(ratings.keys()) # all programs
all_time_slots = list(range(6, 24)) # time slots

######################################### DEFINING FUNCTIONS ########################################################################
# defining fitness function
def fitness_function(schedule):
    total_rating = 0
    for time_slot, program in enumerate(schedule):
        total_rating += ratings[program][time_slot]
    return total_rating

# initializing the population
def initialize_pop(programs, time_slots):
    if not programs:
        return [[]]

    all_schedules = []
    for i in range(len(programs)):
        for schedule in initialize_pop(programs[:i] + programs[i + 1:], time_slots):
            all_schedules.append([programs[i]] + schedule)

    return all_schedules

# selection
def finding_best_schedule(all_schedules):
    best_schedule = []
    max_ratings = 0

    for schedule in all_schedules:
        total_ratings = fitness_function(schedule)
        if total_ratings > max_ratings:
            max_ratings = total_ratings
            best_schedule = schedule

    return best_schedule

# calling the pop func.
all_possible_schedules = initialize_pop(all_programs, all_time_slots)

# callin the schedule func.
best_schedule = finding_best_schedule(all_possible_schedules)


############################################# GENETIC ALGORITHM #############################################################################

# Crossover 
def crossover(schedule1, schedule2):
    crossover_point = random.randint(1, len(schedule1) - 2)
    child1 = schedule1[:crossover_point] + schedule2[crossover_point:]
    child2 = schedule2[:crossover_point] + schedule1[crossover_point:]
    return child1, child2

# mutating
def mutate(schedule):
    mutation_point = random.randint(0, len(schedule) - 1)
    new_program = random.choice(all_programs)
    schedule[mutation_point] = new_program
    return schedule

# calling the fitness func.
def evaluate_fitness(schedule):
    return fitness_function(schedule)

# genetic algorithms with parameters



def genetic_algorithm(initial_schedule, generations=GEN, population_size=POP, crossover_rate=CO_R, mutation_rate=MUT_R, elitism_size=EL_S):
    
    population = [initial_schedule]

    for _ in range(population_size - 1):
        random_schedule = initial_schedule.copy()
        random.shuffle(random_schedule)
        population.append(random_schedule)

    for generation in range(generations):
        new_population = []

        # Elitsm
        population.sort(key=lambda schedule: fitness_function(schedule), reverse=True)
        new_population.extend(population[:elitism_size])

        while len(new_population) < population_size:
            parent1, parent2 = random.choices(population, k=2)
            if random.random() < crossover_rate:
                child1, child2 = crossover(parent1, parent2)
            else:
                child1, child2 = parent1.copy(), parent2.copy()

            if random.random() < mutation_rate:
                child1 = mutate(child1)
            if random.random() < mutation_rate:
                child2 = mutate(child2)

            new_population.extend([child1, child2])

        population = new_population

    return population[0]
  
##################################################### RESULTS ###################################################################################

# brute force
initial_best_schedule = finding_best_schedule(all_possible_schedules)

rem_t_slots = len(all_time_slots) - len(initial_best_schedule)
genetic_schedule = genetic_algorithm(initial_best_schedule, generations=GEN, population_size=POP, elitism_size=EL_S)

final_schedule = initial_best_schedule + genetic_schedule[:rem_t_slots]

print("\nFinal Optimal Schedule:")
for time_slot, program in enumerate(final_schedule):
    print(f"Time Slot {all_time_slots[time_slot]:02d}:00 - Program {program}")

print("Total Ratings:", fitness_function(final_schedule))

Optimizing TV Programs Scheduling Using Genetic Algorithms in Python was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.

A hands-on tutorial explaining how to optimize TV program scheduling using Genetic Algorithm in Python

Photo by Glenn Carstens-Peters on Unsplash