Solving Nonograms with 120 Lines of Code | by Hennie de Harder | Jul, 2022

Puzzles, combinations and solution gifs.

In this post, a way to solve Nonograms without any errors is shown by calculating the options for every line. It’s not the most efficient way to come to a solution, in the end you can find more information about the fastest way. In my opinion, this is the most fun way because it leaves no room for mistakes. And as a bonus, you’ll learn a bit more about counting problems! Let’s jump in!

A Nonogram (aka Griddler, Paint By Numbers, Hanjie or Picross) is a puzzle in which you try to reveal a picture. It’s a logic puzzle with simple rules. You have a grid with squares, and every square should become black or white. Numbers on the side and top of the grid reveal the groups of black squares that should be in every row and column.

Solving Process

Let’s start with an empty Nonogram:

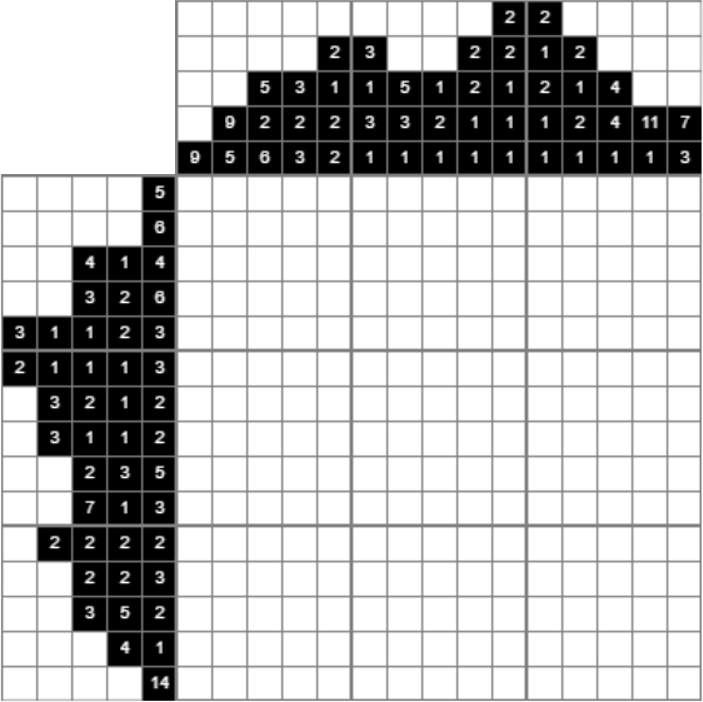
The third column has the values 5, 2 and 6. This indicates there are sets of five, two, and six filled squares, in that order, with at least one blank square between successive sets. Because 5 + 1 (white square) + 2 + 1 (white square)+ 6 is equal to 15, this line is easy to solve, there is only one possible solution:

The dots are helping marks to indicate that these squares should be empty.

Let’s continue. The lowest line contains a group of 14 black squares, and because the total line is 15 squares long, we can fill all squares besides the first and the last one:

We can use these filled squares, because they correspond with the column values on the bottom:

Got it? By using some logic it’s pretty easy to solve this Nonogram! You can try this one by yourself or continue reading and let the computer solve it for you.

Spoiler alert: a gif will show the solving process of this Nonogram at the end.

After understanding the rules of the game, how can we let the computer solve Nonograms using math?

The program consists of three steps. The first step only happens at the beginning and is the most complicated one, while step 2 and step 3 are easy to understand and will be repeated until the puzzle is solved.

Step 1. Calculate all options for every row and column

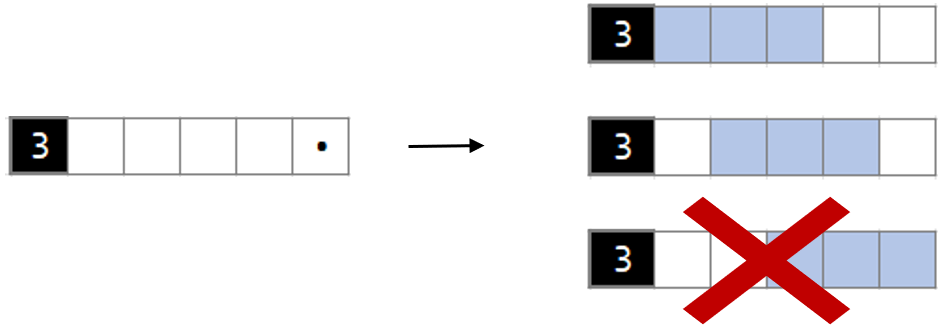
We start by calculating all options to select black squares for every row and column (the next section explains how to do this if things get more complicated). This only happens at the beginning of the game. Let’s say we have a row of five squares and we want to fill it with one group of three:

This gives us the three options on the right.

Step 2. Fill squares that have only one possibility

If you look at the options for one row and you discover that there is only one possibility for a certain square, because in all options the square is black or in all options the square is white, the square can only be filled with this color. This example illustrates this:

Step 3. Remove options from the corresponding row or column

After filling a square (or making it white), we can look at the corresponding row or column and remove all options in which this square is the other color. Because these options aren’t possible anymore. Example:

How to calculate all options for every row and column?

The calculation of options was easy in the example above, we slide the group of three to the left until we reach the end of the row. But what happens if we take a more complicated list with values and try to find all possible options? Another example:

In the example above we place the groups 3, 2 and 6 in a row with 15 squares. We need at least 13 squares for this combination of groups:
6 + 1 white square + 3 + 1 white square + 2 = 13
This means we have 2 empty squares left (15 minus 13 = 2).

An interesting thing to notice is that for the number of total options you only need to know the number of empty squares left and the number of groups you got. An intuitive proof:

Okay, we are making progress! In this example we see that if we got three groups with values (6, 2, 3 on the left and 1, 1, 1 on the right), and two empty squares left, the total number of possible options is 10.

If we forget about the white squares between groups (those should be there no matter what), we can calculate the number of options using combinations. We got 5 places (3 groups + 2 empty squares) and need to select 3 out of 5 (we want to place 3 groups). Here you can find a bit more about combinations. It’s easy to calculate all combinations using python and itertools.

from itertools import combinationsopts = combinations(range(n_groups+n_empty), n_groups)

This also works for the 3, 2, 6 values, except we now place more ones at the places:

That’s it! This works for all groups of values. We only need the number of empty squares left and the number of groups to create all possible options using combinations.

There’s no need to solve a Nonogram by hand after the creation of this program. Let’s solve some Nonograms! 🤓

Let’s start with a small one:

Can it solve the Nonogram we started with?

Yes, of course!

And the final one, what about a really large Nonogram?

Works pretty fast too! 😀👌

Want to solve Nonograms using this program? Below you can find a gist with python code. You only need to specify the row values as a list of lists and the column values as a list of lists. If you call the NonogramSolver class it will start solving your Nonogram. You can choose to save all the steps by specifying the savepath variable.

The Nonogram solver we created has some benefits: it will never fill a square it’s not completely certain about. The downside of this approach is computation time. If the puzzles become larger, more options are available for the rows and columns and the time it takes to solve the puzzle will become longer. Another downside is that it can’t solve Nonograms with multiple solutions.

Luckily, some people already solved these problems. So if you are looking for a super fast Nonogram solver that can handle Nonograms with more solutions, you might find this article interesting.

Don’t forget to subscribe if you’d like to get an email whenever I publish a new article.

Puzzles, combinations and solution gifs.

In this post, a way to solve Nonograms without any errors is shown by calculating the options for every line. It’s not the most efficient way to come to a solution, in the end you can find more information about the fastest way. In my opinion, this is the most fun way because it leaves no room for mistakes. And as a bonus, you’ll learn a bit more about counting problems! Let’s jump in!

A Nonogram (aka Griddler, Paint By Numbers, Hanjie or Picross) is a puzzle in which you try to reveal a picture. It’s a logic puzzle with simple rules. You have a grid with squares, and every square should become black or white. Numbers on the side and top of the grid reveal the groups of black squares that should be in every row and column.

Solving Process

Let’s start with an empty Nonogram:

The third column has the values 5, 2 and 6. This indicates there are sets of five, two, and six filled squares, in that order, with at least one blank square between successive sets. Because 5 + 1 (white square) + 2 + 1 (white square)+ 6 is equal to 15, this line is easy to solve, there is only one possible solution:

The dots are helping marks to indicate that these squares should be empty.

Let’s continue. The lowest line contains a group of 14 black squares, and because the total line is 15 squares long, we can fill all squares besides the first and the last one:

We can use these filled squares, because they correspond with the column values on the bottom:

Got it? By using some logic it’s pretty easy to solve this Nonogram! You can try this one by yourself or continue reading and let the computer solve it for you.

Spoiler alert: a gif will show the solving process of this Nonogram at the end.

After understanding the rules of the game, how can we let the computer solve Nonograms using math?

The program consists of three steps. The first step only happens at the beginning and is the most complicated one, while step 2 and step 3 are easy to understand and will be repeated until the puzzle is solved.

Step 1. Calculate all options for every row and column

We start by calculating all options to select black squares for every row and column (the next section explains how to do this if things get more complicated). This only happens at the beginning of the game. Let’s say we have a row of five squares and we want to fill it with one group of three:

This gives us the three options on the right.

Step 2. Fill squares that have only one possibility

If you look at the options for one row and you discover that there is only one possibility for a certain square, because in all options the square is black or in all options the square is white, the square can only be filled with this color. This example illustrates this:

Step 3. Remove options from the corresponding row or column

After filling a square (or making it white), we can look at the corresponding row or column and remove all options in which this square is the other color. Because these options aren’t possible anymore. Example:

How to calculate all options for every row and column?

The calculation of options was easy in the example above, we slide the group of three to the left until we reach the end of the row. But what happens if we take a more complicated list with values and try to find all possible options? Another example:

In the example above we place the groups 3, 2 and 6 in a row with 15 squares. We need at least 13 squares for this combination of groups:
6 + 1 white square + 3 + 1 white square + 2 = 13
This means we have 2 empty squares left (15 minus 13 = 2).

An interesting thing to notice is that for the number of total options you only need to know the number of empty squares left and the number of groups you got. An intuitive proof:

Okay, we are making progress! In this example we see that if we got three groups with values (6, 2, 3 on the left and 1, 1, 1 on the right), and two empty squares left, the total number of possible options is 10.

If we forget about the white squares between groups (those should be there no matter what), we can calculate the number of options using combinations. We got 5 places (3 groups + 2 empty squares) and need to select 3 out of 5 (we want to place 3 groups). Here you can find a bit more about combinations. It’s easy to calculate all combinations using python and itertools.

from itertools import combinationsopts = combinations(range(n_groups+n_empty), n_groups)

This also works for the 3, 2, 6 values, except we now place more ones at the places:

That’s it! This works for all groups of values. We only need the number of empty squares left and the number of groups to create all possible options using combinations.

There’s no need to solve a Nonogram by hand after the creation of this program. Let’s solve some Nonograms! 🤓

Let’s start with a small one:

Can it solve the Nonogram we started with?

Yes, of course!

And the final one, what about a really large Nonogram?

Works pretty fast too! 😀👌

Want to solve Nonograms using this program? Below you can find a gist with python code. You only need to specify the row values as a list of lists and the column values as a list of lists. If you call the NonogramSolver class it will start solving your Nonogram. You can choose to save all the steps by specifying the savepath variable.

The Nonogram solver we created has some benefits: it will never fill a square it’s not completely certain about. The downside of this approach is computation time. If the puzzles become larger, more options are available for the rows and columns and the time it takes to solve the puzzle will become longer. Another downside is that it can’t solve Nonograms with multiple solutions.

Luckily, some people already solved these problems. So if you are looking for a super fast Nonogram solver that can handle Nonograms with more solutions, you might find this article interesting.

Don’t forget to subscribe if you’d like to get an email whenever I publish a new article.