An introduction to mixed-integer linear programming: The knapsack problem | by Bruno Scalia C. F. Leite | Jul, 2022
Learn how to solve optimization problems in Python using scipy and pyomo
The knapsack problem is probably one of the first problems one faces when studying integer programming, optimization, or operations research. In this problem, from a given set of items, one must choose the most valuable combination to fit in a knapsack of a certain capacity (weight, volume, or both).
Throughout this article, we will implement the knapsack problem in a relaxed form using scipy and in an integer form using pyomo and the GLPK solver. Learning how to use both frameworks can be much helpful for solving more complex problems in the future, and the knapsack problem is an amazing start.
Those interested can follow along with the complete code available in this example notebook.
When formulating an optimization problem, one must define an objective that is a function of a vector decision variables x and might be subject to some equality and inequality constraints, which are functions of x as well. This objective is usually defined in a minimization sense, therefore the goal is to find its lowest value while respecting the constraints. Maximization objectives can be formulated by simply multiplying the corresponding minimization objectives by -1. Lower and upper boundaries for each component of x might be explicit in the formulation, which reduces the search space. As a convention, due to solution techniques, usually lower bounds for decision variables are by default equal to zero.
As both the objective and constraints of a linear problem are linear combinations of its decision variables, the problem can be stated as the following.
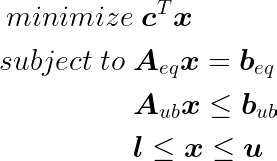
When defining a relaxed formulation, one implies that the original problem has some integer decision variables, and the relaxed form converts those into continuous variables. This is exactly what will occur in this first section. So let us first define the elements of the knapsack problem.
Decision variables:
- x: Column vector with the amount of each item added to the knapsack. In this example, it will be bounded by [0, 1].
Fixed parameters:
- c: Cost associated with each decision variable (negative of its value).
- A_{ub}: Matrix of inequality constraint terms.
- a_{1, i}: Weight per unit of item i.
- a_{2, i}: Volume per unit of item i.
- b_{ub}: Column vector with knapsack weight and volume capacities.
Let us create these elements in Python. First, using dicts, which will be useful later in pyomo. Here I’m using a fixed random seed to obtain the same results always in the random generation.
#Import numpy
import numpy as np#Set of items
I = set(range(1, 11))#Random seed
np.random.seed(12)#Weight associated with each item
w = dict(zip(I, np.random.normal(loc=5.0, scale=1.0, size=10).clip(0.5, 10.0)))#Volume associated with each item
v = dict(zip(I, np.random.normal(loc=6.0, scale=2.0, size=10).clip(0.5, 10.0)))#Price associated with each item
price = dict(zip(I, np.random.normal(loc=10.0, scale=1.0, size=10).clip(0.5, 20.0)))#knapsack capacity
kw, kv = 21.0, 22.0
Then in numpy style to use in scipy.
#Costs
c = -np.array(list(price.values()))#Inequality constraints matrix
A_ub = np.array([
np.array(list(w.values())),
np.array(list(v.values()))
])#Upper bounds for linear inequality constraints
b_ub = np.array([kw, kv])#Bounds (one quantity of each item)
bounds = [(0, 1),] * 10
Now we have all the necessary elements to solve this problem using linprog from scipy.
#Import linprog
from scipy.optimize import linprog#Obtain solution
sol = linprog(c, A_ub=A_ub, b_ub=b_ub, bounds=bounds)#Print
print(sol)
Which returns the following.
con: array([], dtype=float64)
fun: -44.817244893700625
message: 'Optimization terminated successfully.'
nit: 6
slack: array([-1.68047194e-08, -2.36582025e-08])
status: 0
success: True
x: array([9.99999999e-01, 8.65571091e-01, 7.40355899e-10, 1.00000000e+00, 2.62434803e-10, 2.98795062e-09, 2.33299681e-10, 8.80512141e-01, 9.99999997e-01, 2.05849974e-10])
Notice some items in x are fractional, which in some situations is impossible. Therefore, for those situations, we must find a way to find the best feasible solution using integer values for the decision variables. This is performed using integer programming algorithms, which we will see in the next section.
To formulate this problem using integer variables, we will use pyomo to create algebraic integer linear models that can be interpreted by usual algebraic optimization solvers. So let us start by importing pyomo.
import pyomo.environ as pyo
There are two approaches for modeling a problem in pyomo: Abstract and Concrete models. In the first approach, the algebraic expressions of the problem are defined before some data values are supplied, whereas, in the second, the model instance is created immediately as its elements are defined. You can find more about these approaches in the library documentation or in the book by Bynum et al. (2021). Throughout this article, we will adopt the Concrete model formulation.
model = pyo.ConcreteModel()
In algebraic mathematical optimization statements, one usually defines variables and/or expressions over Sets. In the knapsack problem, we have decision variables and parameters associated with each item. Therefore, we will create a Set of items with one key associated with each item.
#Set of items (previously defined)
I = set(range(1, 11))#As an attribute of the problem
model.I = pyo.Set(initialize=I)
In the second step, we will define some fixed parameters of this problem. They are listed below.
- kw: Weight capacity of the knapsack.
- kv: Volume capacity of the knapsack.
- w_i: Weight associated with each item i in the set I.
- v_i: Volume associated with each item i in the set I.
- c_i: Cost (value) associated with each item i in the set I.
The parameters associated with the knapsack are fixed scalars. Therefore we can instantiate them by the following code.
#knapsack capacity
kw, kv = 21.0, 22.0#Parameters of the knapsack
model.kw = pyo.Param(initialize=kw)
model.kv = pyo.Param(initialize=kv)
However, the parameters associated with each item must be defined for each element in the set I. This can be performed by passing the set as the first argument in the pyo.Param definition. Multiple sets can be passed in this statement if the element defined (variable, parameter, expression, or constraint) is indexed by more than one set. This definition is in the Python *args style.
#Parameters of the items
model.v = pyo.Param(model.I, initialize=v)
model.w = pyo.Param(model.I, initialize=w)
model.c = pyo.Param(model.I, initialize=price)
Remember v, w, and price are Python dicts previously defined of which keys are the elements in I.
Now let us define the decision variables of the problem: the number of items added to the knapsack for each item of our set I. Notice I have defined bounds in [0, 1] as for the relaxed formulation. Therefore, an alternative statement could be defining these variables within pyo.Binary.
model.x = pyo.Var(model.I, within=pyo.Integers, bounds=(0, 1))
Great! Now we have defined both the decision variables and fixed parameters we can define the constraints and the objective of the problem.
The constraints can be formulated by the equations below.
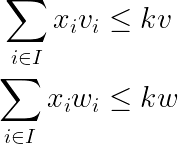
Which is Python goes as.
def weight_constraint(model):
return sum(model.x[i] * model.w[i] for i in model.I) \
<= model.kwmodel.weight_constraint = pyo.Constraint(rule=weight_constraint)def volume_constraint(model):
return sum(model.x[i] * model.v[i] for i in model.I) \
<= model.kvmodel.volume_constraint = pyo.Constraint(rule=volume_constraint)
Notice, that the model is a mandatory argument when creating the functions associated with each constraint. As we pass it to the function, we can reference its attributes previously defined x, w, v, kw, kv, and I.
Now, let us define the objective function. As c was defined as the positive value associated with each item, our objective will be to maximize the value transported in the knapsack.
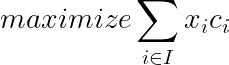
Which in Python goes as the following.
def obj_function(model):
return sum(model.x[i] * model.c[i] for i in model.I)model.objective = pyo.Objective(rule=obj_function, sense=pyo.maximize)
To solve the problem, we must instantiate a solver. In this example, I will use GLPK which is open source, and therefore can be downloaded and executed used by any user. In the field, YOUR_PATH_TO_GLPK, add the path to the glpsol.exe file. For instance, my path is ‘C:\\glpk-4.65\\w64\\glpsol.exe’.
The latest available GLPK version can be found here and the Windows executable files can be found here.
opt = pyo.SolverFactory('glpk', executable=YOUR_PATH_TO_GLPK)#You can add a time limit by using the following command line
opt.options['tmlim'] = 120solution = opt.solve(model)
And we can check the elements of our model now using the display method. For the objective function, see the code below.
model.objective.display()
It should return the following output.
objective : Size=1, Index=None, Active=True
Key : Active : Value
None : True : 39.88187183116921
Therefore, one might notice our integer solution (39.88) is worse than the one obtained using the relaxed formulation (44.82). This occurs in integer problems, as necessarily the decision space is reduced compared to the corresponding space in relaxed problems.
By investigating differences in decision variables, one might notice that:
- Item 1 was added in both situations.
- Item 2 was partially added in the relaxed problem only — value 0.87.
- Item 3 was added only in the integer problem.
- Item 4 was added in both situations.
- Item 5 was not added in any situation.
- Item 6 was not added in any situation.
- Item 7 was not added in any situation.
- Item 8 was partially added in the relaxed problem — value 0.88 — but completely added in the integer version.
- Item 9 was completely added in relaxed problem only.
- Item 10 was not added in any situation.
Those interested in more details about Linear Programming can refer to Luenberger & Ye (2008); for integer programming, see Wolsey (2020); for operations research, Winston & Goldberg (2004).
An extended formulation for the knapsack problem with multiple knapsacks and some additional rules can be found in this other example notebook. I intend to write a Medium article about it soon.
In this article, we have seen an introduction to mixed-integer linear programming. Solutions for the knapsack problem were implemented in a relaxed form using scipy and in an integer form using pyomo and the GLPK solver. The complete code used in these examples is available for further use.
Bynum, M. L. et al., 2021. Pyomo-optimization modeling in python. Springer.
Luenberger, D. G. & Ye, Y., 2008. Linear and Nonlinear Programming. 3rd ed. Stanford: Springer.
Winston, W. L. & Goldberg, J. B., 2004. Operations research: applications and algorithms. 4th ed. Belmont, CA: Thomson Brooks/Cole Belmont.
Wolsey, L. A., 2020. Integer Programming. 2nd ed. John Wiley & Sons.
Learn how to solve optimization problems in Python using scipy and pyomo
The knapsack problem is probably one of the first problems one faces when studying integer programming, optimization, or operations research. In this problem, from a given set of items, one must choose the most valuable combination to fit in a knapsack of a certain capacity (weight, volume, or both).
Throughout this article, we will implement the knapsack problem in a relaxed form using scipy and in an integer form using pyomo and the GLPK solver. Learning how to use both frameworks can be much helpful for solving more complex problems in the future, and the knapsack problem is an amazing start.
Those interested can follow along with the complete code available in this example notebook.
When formulating an optimization problem, one must define an objective that is a function of a vector decision variables x and might be subject to some equality and inequality constraints, which are functions of x as well. This objective is usually defined in a minimization sense, therefore the goal is to find its lowest value while respecting the constraints. Maximization objectives can be formulated by simply multiplying the corresponding minimization objectives by -1. Lower and upper boundaries for each component of x might be explicit in the formulation, which reduces the search space. As a convention, due to solution techniques, usually lower bounds for decision variables are by default equal to zero.
As both the objective and constraints of a linear problem are linear combinations of its decision variables, the problem can be stated as the following.
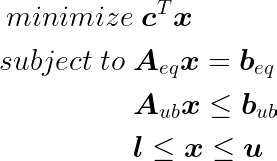
When defining a relaxed formulation, one implies that the original problem has some integer decision variables, and the relaxed form converts those into continuous variables. This is exactly what will occur in this first section. So let us first define the elements of the knapsack problem.
Decision variables:
- x: Column vector with the amount of each item added to the knapsack. In this example, it will be bounded by [0, 1].
Fixed parameters:
- c: Cost associated with each decision variable (negative of its value).
- A_{ub}: Matrix of inequality constraint terms.
- a_{1, i}: Weight per unit of item i.
- a_{2, i}: Volume per unit of item i.
- b_{ub}: Column vector with knapsack weight and volume capacities.
Let us create these elements in Python. First, using dicts, which will be useful later in pyomo. Here I’m using a fixed random seed to obtain the same results always in the random generation.
#Import numpy
import numpy as np#Set of items
I = set(range(1, 11))#Random seed
np.random.seed(12)#Weight associated with each item
w = dict(zip(I, np.random.normal(loc=5.0, scale=1.0, size=10).clip(0.5, 10.0)))#Volume associated with each item
v = dict(zip(I, np.random.normal(loc=6.0, scale=2.0, size=10).clip(0.5, 10.0)))#Price associated with each item
price = dict(zip(I, np.random.normal(loc=10.0, scale=1.0, size=10).clip(0.5, 20.0)))#knapsack capacity
kw, kv = 21.0, 22.0
Then in numpy style to use in scipy.
#Costs
c = -np.array(list(price.values()))#Inequality constraints matrix
A_ub = np.array([
np.array(list(w.values())),
np.array(list(v.values()))
])#Upper bounds for linear inequality constraints
b_ub = np.array([kw, kv])#Bounds (one quantity of each item)
bounds = [(0, 1),] * 10
Now we have all the necessary elements to solve this problem using linprog from scipy.
#Import linprog
from scipy.optimize import linprog#Obtain solution
sol = linprog(c, A_ub=A_ub, b_ub=b_ub, bounds=bounds)#Print
print(sol)
Which returns the following.
con: array([], dtype=float64)
fun: -44.817244893700625
message: 'Optimization terminated successfully.'
nit: 6
slack: array([-1.68047194e-08, -2.36582025e-08])
status: 0
success: True
x: array([9.99999999e-01, 8.65571091e-01, 7.40355899e-10, 1.00000000e+00, 2.62434803e-10, 2.98795062e-09, 2.33299681e-10, 8.80512141e-01, 9.99999997e-01, 2.05849974e-10])
Notice some items in x are fractional, which in some situations is impossible. Therefore, for those situations, we must find a way to find the best feasible solution using integer values for the decision variables. This is performed using integer programming algorithms, which we will see in the next section.
To formulate this problem using integer variables, we will use pyomo to create algebraic integer linear models that can be interpreted by usual algebraic optimization solvers. So let us start by importing pyomo.
import pyomo.environ as pyo
There are two approaches for modeling a problem in pyomo: Abstract and Concrete models. In the first approach, the algebraic expressions of the problem are defined before some data values are supplied, whereas, in the second, the model instance is created immediately as its elements are defined. You can find more about these approaches in the library documentation or in the book by Bynum et al. (2021). Throughout this article, we will adopt the Concrete model formulation.
model = pyo.ConcreteModel()
In algebraic mathematical optimization statements, one usually defines variables and/or expressions over Sets. In the knapsack problem, we have decision variables and parameters associated with each item. Therefore, we will create a Set of items with one key associated with each item.
#Set of items (previously defined)
I = set(range(1, 11))#As an attribute of the problem
model.I = pyo.Set(initialize=I)
In the second step, we will define some fixed parameters of this problem. They are listed below.
- kw: Weight capacity of the knapsack.
- kv: Volume capacity of the knapsack.
- w_i: Weight associated with each item i in the set I.
- v_i: Volume associated with each item i in the set I.
- c_i: Cost (value) associated with each item i in the set I.
The parameters associated with the knapsack are fixed scalars. Therefore we can instantiate them by the following code.
#knapsack capacity
kw, kv = 21.0, 22.0#Parameters of the knapsack
model.kw = pyo.Param(initialize=kw)
model.kv = pyo.Param(initialize=kv)
However, the parameters associated with each item must be defined for each element in the set I. This can be performed by passing the set as the first argument in the pyo.Param definition. Multiple sets can be passed in this statement if the element defined (variable, parameter, expression, or constraint) is indexed by more than one set. This definition is in the Python *args style.
#Parameters of the items
model.v = pyo.Param(model.I, initialize=v)
model.w = pyo.Param(model.I, initialize=w)
model.c = pyo.Param(model.I, initialize=price)
Remember v, w, and price are Python dicts previously defined of which keys are the elements in I.
Now let us define the decision variables of the problem: the number of items added to the knapsack for each item of our set I. Notice I have defined bounds in [0, 1] as for the relaxed formulation. Therefore, an alternative statement could be defining these variables within pyo.Binary.
model.x = pyo.Var(model.I, within=pyo.Integers, bounds=(0, 1))
Great! Now we have defined both the decision variables and fixed parameters we can define the constraints and the objective of the problem.
The constraints can be formulated by the equations below.
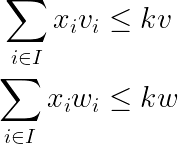
Which is Python goes as.
def weight_constraint(model):
return sum(model.x[i] * model.w[i] for i in model.I) \
<= model.kwmodel.weight_constraint = pyo.Constraint(rule=weight_constraint)def volume_constraint(model):
return sum(model.x[i] * model.v[i] for i in model.I) \
<= model.kvmodel.volume_constraint = pyo.Constraint(rule=volume_constraint)
Notice, that the model is a mandatory argument when creating the functions associated with each constraint. As we pass it to the function, we can reference its attributes previously defined x, w, v, kw, kv, and I.
Now, let us define the objective function. As c was defined as the positive value associated with each item, our objective will be to maximize the value transported in the knapsack.
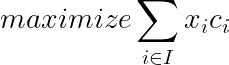
Which in Python goes as the following.
def obj_function(model):
return sum(model.x[i] * model.c[i] for i in model.I)model.objective = pyo.Objective(rule=obj_function, sense=pyo.maximize)
To solve the problem, we must instantiate a solver. In this example, I will use GLPK which is open source, and therefore can be downloaded and executed used by any user. In the field, YOUR_PATH_TO_GLPK, add the path to the glpsol.exe file. For instance, my path is ‘C:\\glpk-4.65\\w64\\glpsol.exe’.
The latest available GLPK version can be found here and the Windows executable files can be found here.
opt = pyo.SolverFactory('glpk', executable=YOUR_PATH_TO_GLPK)#You can add a time limit by using the following command line
opt.options['tmlim'] = 120solution = opt.solve(model)
And we can check the elements of our model now using the display method. For the objective function, see the code below.
model.objective.display()
It should return the following output.
objective : Size=1, Index=None, Active=True
Key : Active : Value
None : True : 39.88187183116921
Therefore, one might notice our integer solution (39.88) is worse than the one obtained using the relaxed formulation (44.82). This occurs in integer problems, as necessarily the decision space is reduced compared to the corresponding space in relaxed problems.
By investigating differences in decision variables, one might notice that:
- Item 1 was added in both situations.
- Item 2 was partially added in the relaxed problem only — value 0.87.
- Item 3 was added only in the integer problem.
- Item 4 was added in both situations.
- Item 5 was not added in any situation.
- Item 6 was not added in any situation.
- Item 7 was not added in any situation.
- Item 8 was partially added in the relaxed problem — value 0.88 — but completely added in the integer version.
- Item 9 was completely added in relaxed problem only.
- Item 10 was not added in any situation.
Those interested in more details about Linear Programming can refer to Luenberger & Ye (2008); for integer programming, see Wolsey (2020); for operations research, Winston & Goldberg (2004).
An extended formulation for the knapsack problem with multiple knapsacks and some additional rules can be found in this other example notebook. I intend to write a Medium article about it soon.
In this article, we have seen an introduction to mixed-integer linear programming. Solutions for the knapsack problem were implemented in a relaxed form using scipy and in an integer form using pyomo and the GLPK solver. The complete code used in these examples is available for further use.
Bynum, M. L. et al., 2021. Pyomo-optimization modeling in python. Springer.
Luenberger, D. G. & Ye, Y., 2008. Linear and Nonlinear Programming. 3rd ed. Stanford: Springer.
Winston, W. L. & Goldberg, J. B., 2004. Operations research: applications and algorithms. 4th ed. Belmont, CA: Thomson Brooks/Cole Belmont.
Wolsey, L. A., 2020. Integer Programming. 2nd ed. John Wiley & Sons.
