Linear Algebra 5: Linear Independence
Ax = 0 and proving a set of vectors is linearly independent
Preface
Welcome back to the fifth edition of my ongoing series on the basics of Linear Algebra, the foundational math behind machine learning. In my previous article, I walked through the matrix equation Ax = b. This essay will investigate the important concept of linear independence and how it connects to everything we’ve learned so far.
This article would best serve readers if read in accompaniment with Linear Algebra and Its Applications by David C. Lay, Steven R. Lay, and Judi J. McDonald. Consider this series as a companion resource.
Feel free to share thoughts, questions, and critique.
Linear Independence in ℝⁿ
Previously, we learned about matrix products and matrix equations in the form Ax = b. We covered that Ax = b has a solution x if b is a linear combination of the set of vectors (columns) in matrix A.
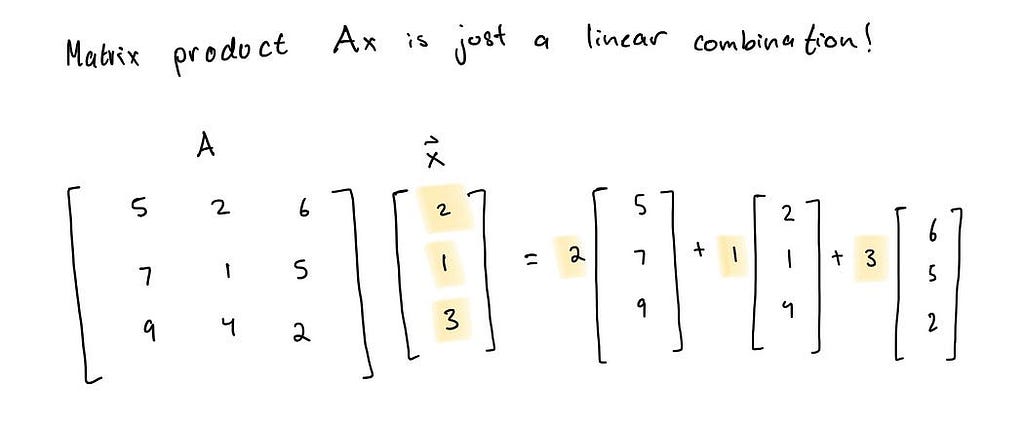
There is a special matrix equation in Linear Algebra Ax = 0 which we refer to as a homogenous linear system. Ax = 0 will always have at least one solution where x = 0 which is called the trivial solution because it is trivially easy to show that any matrix A multiplied by the 0 vector x will result in the 0 vector.
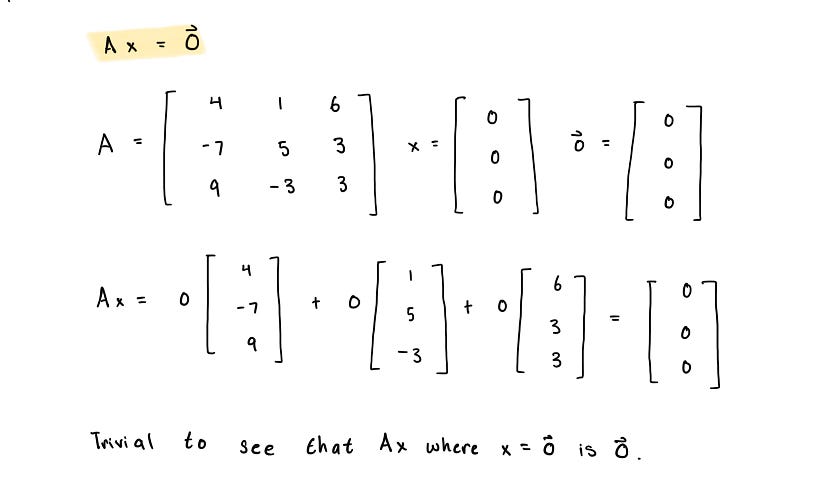
What we’re really interested in learning is whether the matrix equation Ax = 0 has only the trivial solution. If Ax = 0 has only the trivial solution x = 0, then the set of vectors that make up the columns of A are linearly independent. In other words: v₁ + c₂v₂ + … + cₐvₐ = 0 where c₁, c₂, … cₐ must all be 0. A different way of thinking about this is that none of the vectors in the set can be written as a linear combination of another.
On the other hand, if there exists a solution where x ≠ 0 then the set of vectors are linearly dependent. Then it follows that at least one of the vectors in the set can be written as a linear combination of another: c₁v₁ + c₂v₂ + … + cₐvₐ = 0 where not all where c₁, c₂, … cₐ equal 0.
A neat, intuitive way of thinking about the concept of linear independence is the question of can you find a set of weights that will collapse the linear combination of a set of vectors to the origin? If a set of vectors is linearly independent, then 0 is the only weight that can be applied to each vector for the linear combination to equal the zero vector. If the vectors are linearly dependent, then there exists at least one set of non-zero weights such that the vector linear combination is zero.
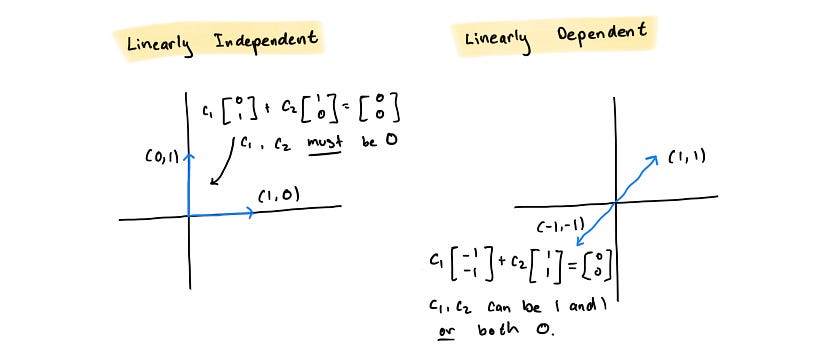
Determining Linear Independence
For sets with only one vector, determining linear independence is trivial. If the vector is the zero vector, then it is linearly dependent. This is because any non-zero weight multiplied to the zero vector will equal the zero vector and so there exists infinitely many solutions for Ax = 0. If the vector is not the zero vector, then the vector is linearly independent since any vector multiplied by zero will become the zero vector.
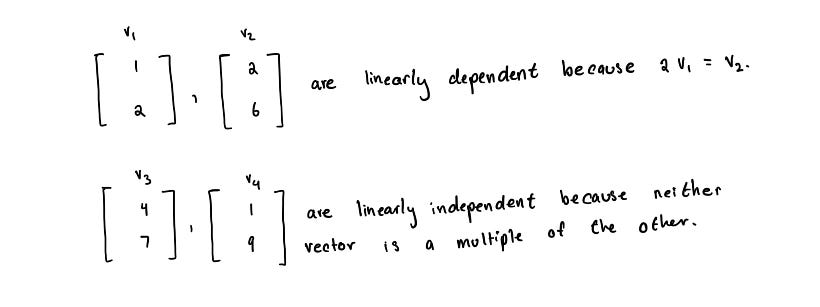
If a set contains two vectors, the vectors are linearly dependent if one vectors is a multiple of the other. Otherwise, they are linearly independent.
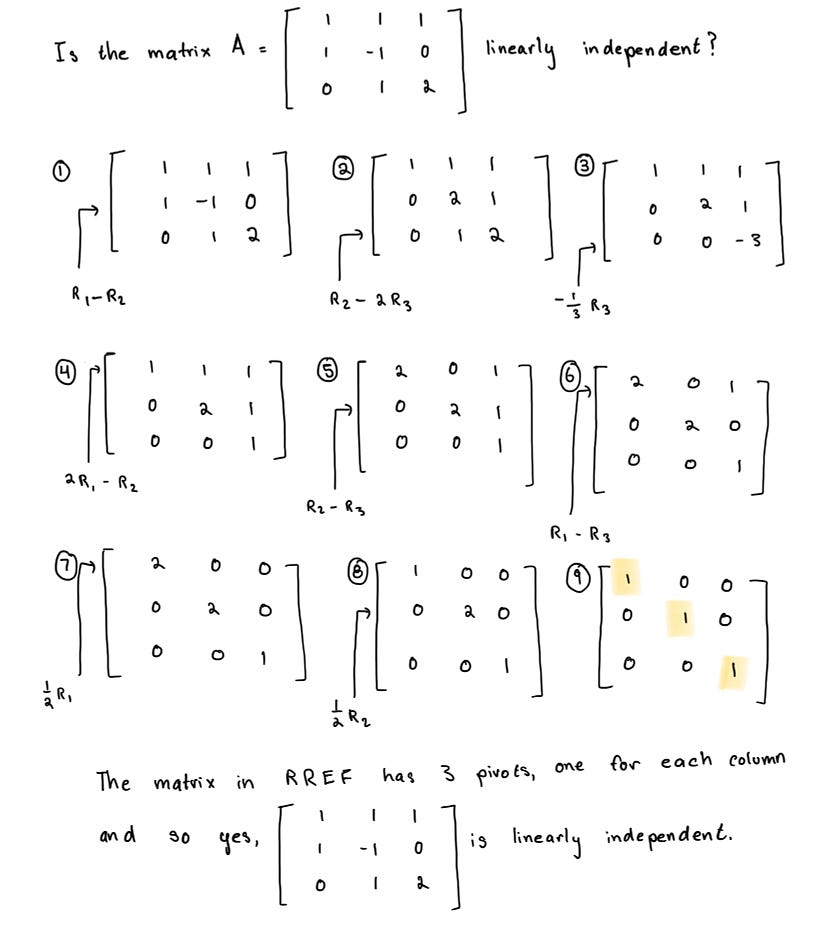
In the case of sets with more than two vectors, more computation is involved. Let the vectors form the columns of matrix A and row reduce matrix A to reduced row echelon form. If the reduced row echelon form of the matrix has a pivot entry in every column, then the set of vectors is linearly independent. Otherwise, the set of vectors is linearly dependent. Why is this the case? Consider the process of row reducing a matrix to its reduced row echelon form. We perform a series of elementary row operations such as multiplying rows by constants, swapping rows, adding one row to another in pursuit of a matrix in a simpler form so that its underlying properties are clear while the solution space is preserved.
In the case of linear independence, the quality of having a pivot in each column indicates that each vector plays a leading role in at least one part of the linear combination equation. If each vector contributes independently to the linear system, then no vector can be expressed as a linear combination of the others and so the system is linearly independent. Conversely, if there is a column in RREF without a pivot entry, it means that the corresponding variable (or vector) is a dependent variable and can be expressed in terms of the other vectors. In other words, there exists a redundancy in the system, indicating linear dependence among the vectors.
A concise way to summarize this idea involves the rank of a matrix. The rank is the maximum number of linearly independent columns in a matrix and so it follows that the rank is equal to the number of pivots in reduced row echelon form.
If the number of columns in a matrix is equal to the rank, then the matrix is linearly independent. Otherwise, the matrix is linearly dependent.

Linear Independence with Numpy
Attempting computations made by hand is a worthwhile exercise in better understanding linear independence, but a more practical approach would be to use the capabilities built into the Numpy library to both test for linear independence and to derive the solution space for Ax = 0 of a given matrix.
We can approach checking if a matrix is linearly independent using the rank. As mentioned previously, a matrix is linearly independent if the rank of a matrix is equal to the number of columns so our code will be written around this criteria.
https://medium.com/media/8650c2b2865233acac74fd3879509a2d/href
The following code generates the solution space of vectors for Ax = 0.
https://medium.com/media/e5b51bc460e3554070c45d485e924ed4/href
Conclusion
Linear independence, while fundamental to Linear Algebra, also serves as a cornerstone in machine learning applications. Linear independence is crucial in feature selection and dimensionality reduction techniques such as principal component analysis (PCA) which operates on the collinearity or linear dependence between features in the dataset.
You’ll continue to see linear independence pop up in machine learning!
Summary
- A system of linear equations is referred to as homogenous if it can be written in the form Ax = 0.
- Linearly independent vectors cannot be expressed as a linear combination of each other (except the trivial combination where all coefficients are zero).
- Linearly dependent vectors are those where at least one vector in the set can be expressed as a linear combination of the others.
- Numpy, a Python library for working with arrays offers fantastic support for both checking if a matrix is linearly independent and also solving Ax = 0 for a given matrix.
Notes
*All images created by the author unless otherwise noted.

Linear Algebra 5: Linear Independence was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
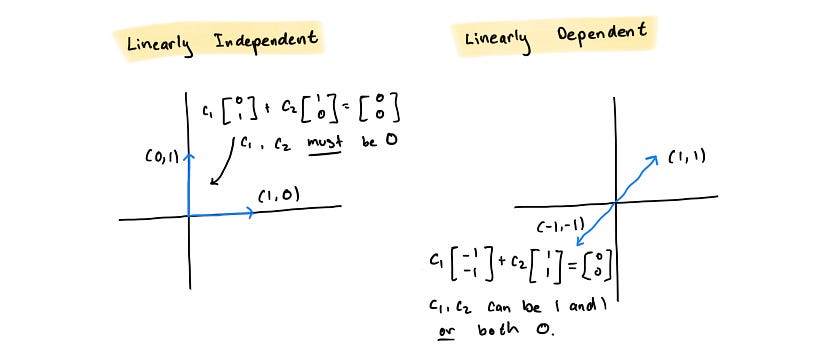
Ax = 0 and proving a set of vectors is linearly independent
Preface
Welcome back to the fifth edition of my ongoing series on the basics of Linear Algebra, the foundational math behind machine learning. In my previous article, I walked through the matrix equation Ax = b. This essay will investigate the important concept of linear independence and how it connects to everything we’ve learned so far.
This article would best serve readers if read in accompaniment with Linear Algebra and Its Applications by David C. Lay, Steven R. Lay, and Judi J. McDonald. Consider this series as a companion resource.
Feel free to share thoughts, questions, and critique.
Linear Independence in ℝⁿ
Previously, we learned about matrix products and matrix equations in the form Ax = b. We covered that Ax = b has a solution x if b is a linear combination of the set of vectors (columns) in matrix A.
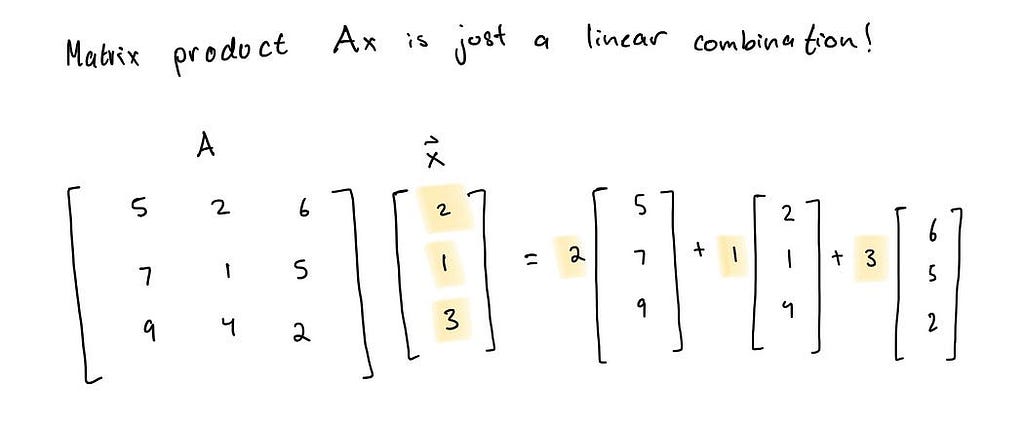
There is a special matrix equation in Linear Algebra Ax = 0 which we refer to as a homogenous linear system. Ax = 0 will always have at least one solution where x = 0 which is called the trivial solution because it is trivially easy to show that any matrix A multiplied by the 0 vector x will result in the 0 vector.

What we’re really interested in learning is whether the matrix equation Ax = 0 has only the trivial solution. If Ax = 0 has only the trivial solution x = 0, then the set of vectors that make up the columns of A are linearly independent. In other words: v₁ + c₂v₂ + … + cₐvₐ = 0 where c₁, c₂, … cₐ must all be 0. A different way of thinking about this is that none of the vectors in the set can be written as a linear combination of another.
On the other hand, if there exists a solution where x ≠ 0 then the set of vectors are linearly dependent. Then it follows that at least one of the vectors in the set can be written as a linear combination of another: c₁v₁ + c₂v₂ + … + cₐvₐ = 0 where not all where c₁, c₂, … cₐ equal 0.
A neat, intuitive way of thinking about the concept of linear independence is the question of can you find a set of weights that will collapse the linear combination of a set of vectors to the origin? If a set of vectors is linearly independent, then 0 is the only weight that can be applied to each vector for the linear combination to equal the zero vector. If the vectors are linearly dependent, then there exists at least one set of non-zero weights such that the vector linear combination is zero.
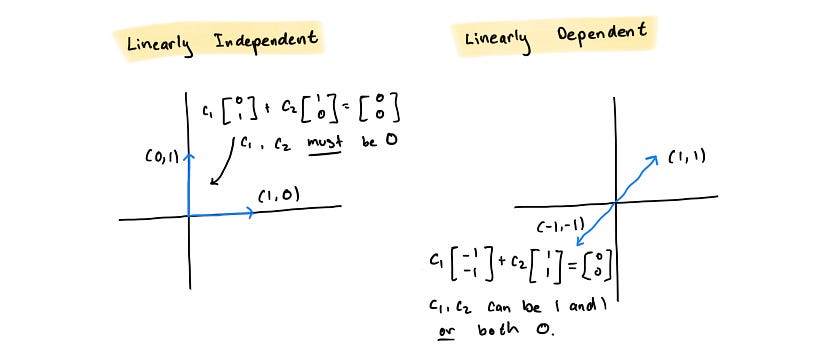
Determining Linear Independence
For sets with only one vector, determining linear independence is trivial. If the vector is the zero vector, then it is linearly dependent. This is because any non-zero weight multiplied to the zero vector will equal the zero vector and so there exists infinitely many solutions for Ax = 0. If the vector is not the zero vector, then the vector is linearly independent since any vector multiplied by zero will become the zero vector.
If a set contains two vectors, the vectors are linearly dependent if one vectors is a multiple of the other. Otherwise, they are linearly independent.

In the case of sets with more than two vectors, more computation is involved. Let the vectors form the columns of matrix A and row reduce matrix A to reduced row echelon form. If the reduced row echelon form of the matrix has a pivot entry in every column, then the set of vectors is linearly independent. Otherwise, the set of vectors is linearly dependent. Why is this the case? Consider the process of row reducing a matrix to its reduced row echelon form. We perform a series of elementary row operations such as multiplying rows by constants, swapping rows, adding one row to another in pursuit of a matrix in a simpler form so that its underlying properties are clear while the solution space is preserved.
In the case of linear independence, the quality of having a pivot in each column indicates that each vector plays a leading role in at least one part of the linear combination equation. If each vector contributes independently to the linear system, then no vector can be expressed as a linear combination of the others and so the system is linearly independent. Conversely, if there is a column in RREF without a pivot entry, it means that the corresponding variable (or vector) is a dependent variable and can be expressed in terms of the other vectors. In other words, there exists a redundancy in the system, indicating linear dependence among the vectors.
A concise way to summarize this idea involves the rank of a matrix. The rank is the maximum number of linearly independent columns in a matrix and so it follows that the rank is equal to the number of pivots in reduced row echelon form.
If the number of columns in a matrix is equal to the rank, then the matrix is linearly independent. Otherwise, the matrix is linearly dependent.


Linear Independence with Numpy
Attempting computations made by hand is a worthwhile exercise in better understanding linear independence, but a more practical approach would be to use the capabilities built into the Numpy library to both test for linear independence and to derive the solution space for Ax = 0 of a given matrix.
We can approach checking if a matrix is linearly independent using the rank. As mentioned previously, a matrix is linearly independent if the rank of a matrix is equal to the number of columns so our code will be written around this criteria.
https://medium.com/media/8650c2b2865233acac74fd3879509a2d/href
The following code generates the solution space of vectors for Ax = 0.
https://medium.com/media/e5b51bc460e3554070c45d485e924ed4/href
Conclusion
Linear independence, while fundamental to Linear Algebra, also serves as a cornerstone in machine learning applications. Linear independence is crucial in feature selection and dimensionality reduction techniques such as principal component analysis (PCA) which operates on the collinearity or linear dependence between features in the dataset.
You’ll continue to see linear independence pop up in machine learning!
Summary
- A system of linear equations is referred to as homogenous if it can be written in the form Ax = 0.
- Linearly independent vectors cannot be expressed as a linear combination of each other (except the trivial combination where all coefficients are zero).
- Linearly dependent vectors are those where at least one vector in the set can be expressed as a linear combination of the others.
- Numpy, a Python library for working with arrays offers fantastic support for both checking if a matrix is linearly independent and also solving Ax = 0 for a given matrix.
Notes
*All images created by the author unless otherwise noted.

Linear Algebra 5: Linear Independence was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
