Multiple linear regression: Theory and applications | by Bruno Scalia C. F. Leite | Sep, 2022
Linear least-squares explained in detail and implemented from scratch in Python
Multiple linear regression is one of the most fundamental statistical models due to its simplicity and interpretability of results. For prediction purposes, linear models can sometimes outperform fancier nonlinear models, especially in situations with small numbers of training cases, low signal-to-noise ratio, or sparse data (Hastie et al., 2009). In these models, as their name suggests, a predicted (or response) variable is described by a linear combination of predictors. The term “multiple refers to the predictor variables.
Throughout this article, the underlying principles of the Ordinary Least-Squares (OLS) regression model will be described in detail, and a regressor will be implemented from scratch in Python. All the code used is available in this example notebook.
Linear regression is already available in many Python frameworks. Therefore, in practice, one does not need to implement it from scratch to estimate regression coefficients and make predictions. However, our goal here is to gain insight into how these models work and their assumptions to be more effective when tackling future projects. From the usual frameworks, I suggest checking OLS from statsmodels and LinearRegression from sklearn.
Let us dive in.
Before diving into equations, I would like to define some notation guidelines.
- Matrices: uppercase italic bold.
- Vectors: lowercase italic bold.
- Scalars: regular italic.
A multiple linear regression model, or an OLS, can be described by the equation below.

In which yᵢ is the dependent variable (or response) of observation i, β₀ is the regression intercept, βⱼ are coefficients associated with decision variables j, xᵢⱼ is the decision variable j of the observation i, and ε is the residual term. In matrix notation, it can be described by:

In which β is a column vector of parameters.
The linear model makes huge assumptions about structure and yields stable but possibly inaccurate predictions (Hastie et al, 2009). When adopting a linear model, one should be aware of these assumptions to make correct inferences about the results and to perform necessary changes.
The residual terms ε are assumed to be normally and independently distributed with mean zero and constant variance σ². Some model properties, such as confidence intervals of parameters and predictions, strongly rely on these assumptions about ε. Verifying them is, therefore, essential to obtain meaningful results.
The goal of the linear least-squares regression model is to find the values for β that minimize the sum of squared residuals (or squared errors), given by the equation below.

This is an optimization problem with analytical solution. The formula is based on the gradient of each prediction with respect to the vector of parameters β, which corresponds to the vector of independent variables itself xᵢ. Consider a matrix C, given by the equation below.

The least-squares estimate of β is given by:

Let us, in the next steps, create a Python class, LinearRegression, to perform these estimations. But before, let us import some useful libraries and functions to use throughout this article.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.stats import shapiro
from scipy.stats import t as t_fun
The first step is to create an estimator class and a method to include a column of ones in the matrix of estimators if we want to consider an intercept β₀.
class LinearRegression: def __init__(self, fit_intercept=True):
self.fit_intercept = fit_intercept def _prepare_X(self, X):
X = np.array(X) if len(X.shape) == 1:
X = np.atleast_2d(X).reshape((-1, 1)) if self.fit_intercept:
ones = np.ones((X.shape[0], 1))
X = np.column_stack((ones, X))
else:
pass return X
Now, let us implement a fit method (sklearn-like) to estimate β.
def fit(self, X, y=None): X = self._prepare_X(X)
n, p = X.shape
self.n = n
self.p = p C = np.linalg.inv(X.T.dot(X))
self.C = C
betas = C.dot(X.T.dot(y))
self.betas = betas
A method for predictions.
def predict(self, X, y=None): X = self._prepare_X(X)
y_pred = X.dot(self.betas) return y_pred
And a method for computing the R² metric.
def r2_score(self, X, y): y_pred = self.predict(X)
epsilon = y_pred - y
sse = np.sum(epsilon * epsilon) y_mean = np.mean(y)
mean_res = y_mean - y
sst = np.sum(mean_res * mean_res) return 1 - sse / sst
It is useful to test the statistical significance of parameters β to verify the relevance of a predictor. When doing so, we are able to remove poor predictors, avoid confounding effects, and improve model performance on new predictions. To do so, one should test the null hypothesis that the parameter β associated with a given predictor is zero. Let us compute the variance-covariance matrix V of the parameters β and their corresponding standard errors using the matrix C and the variance of residuals σ̂².
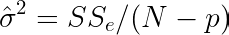
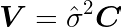

In Python, we can just add the following lines to the fit method:
epsilon = y - X.dot(betas)
sse = np.sum(epsilon * epsilon)sigma_squared = sse / (n - p)
self.sigma_squared = sigma_squaredV = C * sigma_squared
self.V = Vsigma_betas = np.sqrt(np.diag(V))
self.sigma_betas = sigma_betas
Then, we might get the t-value associated with the null hypothesis and its corresponding p-value. In Python, it can be done by using the t generator instance from scipy.stats (previously imported here as t_fun).
pvalues = t_fun.sf(abs(betas) / sigma_betas, (n - p)) * 2.0
self.pvalues = pvalues
Now we have our tools ready to estimate regression coefficients and their statistical significance and to make predictions from new observations. Let us apply this framework in the next section.
This is an example in which the goal is to predict the pull strength of a wire bond in a semiconductor manufacturing process based on wire length and die height. It was retrieved from Montgomery & Runger (2003). This is a small dataset, a situation in which linear models can be especially useful. I saved a copy of it in a .txt file in the same repository as the example notebook.
Let us first import the dataset.
dataset = pd.read_csv("../data/montgomery/wire_bond.txt", sep=" ", index_col=0)
And then define the matrix of independent variables X and the vector of the observed values of the predicted variable y.
X = dataset.iloc[:, :-1].values
y = dataset.iloc[:, -1].values
I’ve created a few scatter plots to see how the predictors are related to the dependent variable.

Notice that a strong linear relationship exists between the predicted variable and the regressor wire length. Conversely, the linear relationship between die height and wire bond is not so evident in the pairwise visualization, although this might be attributed to the effects of the other predictor.
Next, let us create an instance of the LinearRegression class, fit it to the data, and verify its performance based on the R² metric.
linreg = LinearRegression()
linreg.fit(X, y)print(linreg.r2_score(X, y))
Which returns the value of 0.9811.
It seems promising! Now, to verify the statistical significance of the parameters, let us run the following code:
for i, val in enumerate(linreg.betas):
pval = linreg.pvalues[i]
print(f"Beta {i}: {val:.2f}; p-value: {pval:.2f}")
Which returns:
Beta 0: 2.26; p-value: 0.04
Beta 1: 2.74; p-value: 0.00
Beta 2: 0.01; p-value: 0.00
Therefore, we have a model with great performance and statistical significance, which is likely to perform well on new observations as long as data distribution does not significantly change. Notice that, according to its p-value, we might consider dropping the intercept. Finally, let us verify the model assumptions.
- Residuals are normally and independently distributed.
- The mean of residuals is zero.
- Residuals have constant variance.
Let us first verify the mean of residuals.
y_hat = linreg.predict(X)
epsilon = y - y_hat
print(f"Mean epsilon: {np.mean(epsilon):.3f}")
print(f"Sigma epsilon: {np.std(epsilon):.3f}")
Which seems okay:
Mean epsilon: -0.000
Sigma epsilon: 2.146
And now, let us use the Shapiro-Wilk test for normality.
shapiro_stat, shapiro_pvalue = shapiro(epsilon)
print(f"Shapiro test p-value: {shapiro_pvalue:.2f}")
Which returns:
Shapiro test p-value: 0.38
Therefore, we can not reject the null hypothesis that our residuals come from a normal distribution.
Finally, let us plot the residuals versus the predicted variable and regressors to verify if they are independently distributed.


The residuals are mostly well distributed, especially in the region of wire length below seven and target below 25. However, there might exist some nonlinearity between the target and wire length as the residuals in intermediate values are biased towards negative values, whereas high values (target > 50) are biased towards positive values. Those interested in exploring the problem in more detail might try to create polynomial features and see if this bias is reduced. Moreover, the variance does not seem to be conditionally distributed. Therefore, it is unlikely that we could improve model performance by weighting residuals.
In the next section, let us create a false predictor correlated to the first independent variable and verify if the statistical significance test can identify it.
The false predictor will be equal to the wire length added to a random noise term following a normal distribution of mean zero and sigma one.
# Predefined random seed to reproductibility of results
np.random.seed(42)# Create feature
x_false = X[:, 0] + np.random.randn(X.shape[0])
X_false = np.column_stack((X, x_false.reshape((-1, 1))))
Notice that it is also linearly correlated to the response variable. In fact, even more correlated than the die height.

Let us repeat the process from the previous section to see the results.
linreg_alt = LinearRegression()
linreg_alt.fit(X_false, y)
print(linreg_alt.r2_score(X_false, y))
It seems the scoring metric is still great (0.9828), but not necessarily our results are meaningful as before. Let us verify the confidence intervals.
for i, val in enumerate(linreg_alt.betas):
pval = linreg_alt.pvalues[i]
print(f"Beta {i}: {val:.2f}; p-value: {pval:.2f}")
Which returns:
Beta 0: 2.13; p-value: 0.05
Beta 1: 3.43; p-value: 0.00
Beta 2: 0.01; p-value: 0.00
Beta 3: -0.69; p-value: 0.16
And it seems we found the impostor…
Therefore, our framework effectively verifies that the false predictor does not provide additional information to the model, given that we still have the original values of wire length, even though the false predictor has a strong linear correlation to the predicted variable. Conversely, the die height, which has a weaker correlation, contributes to the model with statistical significance.
In such situations, removing unnecessary features from the model is highly recommended to improve its interpretability and generality. In the example notebook, I also present a strategy for recursive feature elimination based on p-values.
As one with an Engineering background, the first reference I should recommend in the area is the book Applied Statistics and Probability for Engineers by Montgomery & Runger (2003). There, one might find a more detailed description of the fundamentals herein presented and other relevant regression aspects such as multicollinearity, confidence intervals on the mean response, and feature selection.
Those more interested in Machine Learning can refer to The Elements of Statistical Learning by Hastie et al. (2009). In particular, I find it very interesting to see how the authors explain the bias-variance trade-off comparing nearest neighbors to linear models.
Nonlinear regression is also fascinating when one aims to estimate parameters with some fundamental meaning to describe nonlinear phenomena. The book Nonlinear Regression Analysis and Its Applications by Bates & Watts (1988) is a great reference. The subject is also presented in Chapter 3 of the book Generalized Linear Models by Myers et al. (2010).
Lecture notes by professor Cosma Shalizi are available on this link. Currently, the draft is under the title of Advanced Data Analysis from an Elementary Point of View. There, one can find interesting subjects such as Weighting and Variance, Causal Inference, and Dependent Data.
I appreciate the Python package statsmodels. After applying OLS (as we performed in this article), one might be interested in trying WLS for problems with uneven variance of residuals and using VIF for detecting feature multicollinearity.
In this article, the main principles of multiple linear regression were presented, followed by implementation from scratch in Python. The framework was applied to a simple example, in which the statistical significance of parameters was verified besides the main assumptions about residuals in linear least-squares problems. The complete code and additional examples are available in this link.
Bates, D. M. & Watts, D. G., 1988. Nonlinear Regression Analysis and Its Applications. Wiley.
Hastie, T., Tibshirani, R. & Friedman, J. H., 2009. The Elements of Statistical Learning: Data mining, Inference, and Prediction. 2nd ed. New York: Springer.
Montgomery, D. C. & Runger, G., 2003. Applied Statistics and Probability for Engineers. 3rd ed. John Wiley and Sons.
Myers, R. H., Montgomery, D. C., Vining, G. G. & Robinson, T. J., 2012. Generalized linear models: with applications in engineering and the sciences. 2nd ed. Hoboken: John Wiley & Sons.
Shalizi, C., 2021. Advanced Data Analysis from an Elementary Point of View. Cambridge University Press.
Linear least-squares explained in detail and implemented from scratch in Python
Multiple linear regression is one of the most fundamental statistical models due to its simplicity and interpretability of results. For prediction purposes, linear models can sometimes outperform fancier nonlinear models, especially in situations with small numbers of training cases, low signal-to-noise ratio, or sparse data (Hastie et al., 2009). In these models, as their name suggests, a predicted (or response) variable is described by a linear combination of predictors. The term “multiple refers to the predictor variables.
Throughout this article, the underlying principles of the Ordinary Least-Squares (OLS) regression model will be described in detail, and a regressor will be implemented from scratch in Python. All the code used is available in this example notebook.
Linear regression is already available in many Python frameworks. Therefore, in practice, one does not need to implement it from scratch to estimate regression coefficients and make predictions. However, our goal here is to gain insight into how these models work and their assumptions to be more effective when tackling future projects. From the usual frameworks, I suggest checking OLS from statsmodels and LinearRegression from sklearn.
Let us dive in.
Before diving into equations, I would like to define some notation guidelines.
- Matrices: uppercase italic bold.
- Vectors: lowercase italic bold.
- Scalars: regular italic.
A multiple linear regression model, or an OLS, can be described by the equation below.

In which yᵢ is the dependent variable (or response) of observation i, β₀ is the regression intercept, βⱼ are coefficients associated with decision variables j, xᵢⱼ is the decision variable j of the observation i, and ε is the residual term. In matrix notation, it can be described by:

In which β is a column vector of parameters.
The linear model makes huge assumptions about structure and yields stable but possibly inaccurate predictions (Hastie et al, 2009). When adopting a linear model, one should be aware of these assumptions to make correct inferences about the results and to perform necessary changes.
The residual terms ε are assumed to be normally and independently distributed with mean zero and constant variance σ². Some model properties, such as confidence intervals of parameters and predictions, strongly rely on these assumptions about ε. Verifying them is, therefore, essential to obtain meaningful results.
The goal of the linear least-squares regression model is to find the values for β that minimize the sum of squared residuals (or squared errors), given by the equation below.

This is an optimization problem with analytical solution. The formula is based on the gradient of each prediction with respect to the vector of parameters β, which corresponds to the vector of independent variables itself xᵢ. Consider a matrix C, given by the equation below.

The least-squares estimate of β is given by:

Let us, in the next steps, create a Python class, LinearRegression, to perform these estimations. But before, let us import some useful libraries and functions to use throughout this article.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.stats import shapiro
from scipy.stats import t as t_fun
The first step is to create an estimator class and a method to include a column of ones in the matrix of estimators if we want to consider an intercept β₀.
class LinearRegression: def __init__(self, fit_intercept=True):
self.fit_intercept = fit_intercept def _prepare_X(self, X):
X = np.array(X) if len(X.shape) == 1:
X = np.atleast_2d(X).reshape((-1, 1)) if self.fit_intercept:
ones = np.ones((X.shape[0], 1))
X = np.column_stack((ones, X))
else:
pass return X
Now, let us implement a fit method (sklearn-like) to estimate β.
def fit(self, X, y=None): X = self._prepare_X(X)
n, p = X.shape
self.n = n
self.p = p C = np.linalg.inv(X.T.dot(X))
self.C = C
betas = C.dot(X.T.dot(y))
self.betas = betas
A method for predictions.
def predict(self, X, y=None): X = self._prepare_X(X)
y_pred = X.dot(self.betas) return y_pred
And a method for computing the R² metric.
def r2_score(self, X, y): y_pred = self.predict(X)
epsilon = y_pred - y
sse = np.sum(epsilon * epsilon) y_mean = np.mean(y)
mean_res = y_mean - y
sst = np.sum(mean_res * mean_res) return 1 - sse / sst
It is useful to test the statistical significance of parameters β to verify the relevance of a predictor. When doing so, we are able to remove poor predictors, avoid confounding effects, and improve model performance on new predictions. To do so, one should test the null hypothesis that the parameter β associated with a given predictor is zero. Let us compute the variance-covariance matrix V of the parameters β and their corresponding standard errors using the matrix C and the variance of residuals σ̂².
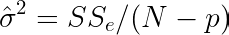
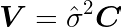

In Python, we can just add the following lines to the fit method:
epsilon = y - X.dot(betas)
sse = np.sum(epsilon * epsilon)sigma_squared = sse / (n - p)
self.sigma_squared = sigma_squaredV = C * sigma_squared
self.V = Vsigma_betas = np.sqrt(np.diag(V))
self.sigma_betas = sigma_betas
Then, we might get the t-value associated with the null hypothesis and its corresponding p-value. In Python, it can be done by using the t generator instance from scipy.stats (previously imported here as t_fun).
pvalues = t_fun.sf(abs(betas) / sigma_betas, (n - p)) * 2.0
self.pvalues = pvalues
Now we have our tools ready to estimate regression coefficients and their statistical significance and to make predictions from new observations. Let us apply this framework in the next section.
This is an example in which the goal is to predict the pull strength of a wire bond in a semiconductor manufacturing process based on wire length and die height. It was retrieved from Montgomery & Runger (2003). This is a small dataset, a situation in which linear models can be especially useful. I saved a copy of it in a .txt file in the same repository as the example notebook.
Let us first import the dataset.
dataset = pd.read_csv("../data/montgomery/wire_bond.txt", sep=" ", index_col=0)
And then define the matrix of independent variables X and the vector of the observed values of the predicted variable y.
X = dataset.iloc[:, :-1].values
y = dataset.iloc[:, -1].values
I’ve created a few scatter plots to see how the predictors are related to the dependent variable.

Notice that a strong linear relationship exists between the predicted variable and the regressor wire length. Conversely, the linear relationship between die height and wire bond is not so evident in the pairwise visualization, although this might be attributed to the effects of the other predictor.
Next, let us create an instance of the LinearRegression class, fit it to the data, and verify its performance based on the R² metric.
linreg = LinearRegression()
linreg.fit(X, y)print(linreg.r2_score(X, y))
Which returns the value of 0.9811.
It seems promising! Now, to verify the statistical significance of the parameters, let us run the following code:
for i, val in enumerate(linreg.betas):
pval = linreg.pvalues[i]
print(f"Beta {i}: {val:.2f}; p-value: {pval:.2f}")
Which returns:
Beta 0: 2.26; p-value: 0.04
Beta 1: 2.74; p-value: 0.00
Beta 2: 0.01; p-value: 0.00
Therefore, we have a model with great performance and statistical significance, which is likely to perform well on new observations as long as data distribution does not significantly change. Notice that, according to its p-value, we might consider dropping the intercept. Finally, let us verify the model assumptions.
- Residuals are normally and independently distributed.
- The mean of residuals is zero.
- Residuals have constant variance.
Let us first verify the mean of residuals.
y_hat = linreg.predict(X)
epsilon = y - y_hat
print(f"Mean epsilon: {np.mean(epsilon):.3f}")
print(f"Sigma epsilon: {np.std(epsilon):.3f}")
Which seems okay:
Mean epsilon: -0.000
Sigma epsilon: 2.146
And now, let us use the Shapiro-Wilk test for normality.
shapiro_stat, shapiro_pvalue = shapiro(epsilon)
print(f"Shapiro test p-value: {shapiro_pvalue:.2f}")
Which returns:
Shapiro test p-value: 0.38
Therefore, we can not reject the null hypothesis that our residuals come from a normal distribution.
Finally, let us plot the residuals versus the predicted variable and regressors to verify if they are independently distributed.


The residuals are mostly well distributed, especially in the region of wire length below seven and target below 25. However, there might exist some nonlinearity between the target and wire length as the residuals in intermediate values are biased towards negative values, whereas high values (target > 50) are biased towards positive values. Those interested in exploring the problem in more detail might try to create polynomial features and see if this bias is reduced. Moreover, the variance does not seem to be conditionally distributed. Therefore, it is unlikely that we could improve model performance by weighting residuals.
In the next section, let us create a false predictor correlated to the first independent variable and verify if the statistical significance test can identify it.
The false predictor will be equal to the wire length added to a random noise term following a normal distribution of mean zero and sigma one.
# Predefined random seed to reproductibility of results
np.random.seed(42)# Create feature
x_false = X[:, 0] + np.random.randn(X.shape[0])
X_false = np.column_stack((X, x_false.reshape((-1, 1))))
Notice that it is also linearly correlated to the response variable. In fact, even more correlated than the die height.

Let us repeat the process from the previous section to see the results.
linreg_alt = LinearRegression()
linreg_alt.fit(X_false, y)
print(linreg_alt.r2_score(X_false, y))
It seems the scoring metric is still great (0.9828), but not necessarily our results are meaningful as before. Let us verify the confidence intervals.
for i, val in enumerate(linreg_alt.betas):
pval = linreg_alt.pvalues[i]
print(f"Beta {i}: {val:.2f}; p-value: {pval:.2f}")
Which returns:
Beta 0: 2.13; p-value: 0.05
Beta 1: 3.43; p-value: 0.00
Beta 2: 0.01; p-value: 0.00
Beta 3: -0.69; p-value: 0.16
And it seems we found the impostor…
Therefore, our framework effectively verifies that the false predictor does not provide additional information to the model, given that we still have the original values of wire length, even though the false predictor has a strong linear correlation to the predicted variable. Conversely, the die height, which has a weaker correlation, contributes to the model with statistical significance.
In such situations, removing unnecessary features from the model is highly recommended to improve its interpretability and generality. In the example notebook, I also present a strategy for recursive feature elimination based on p-values.
As one with an Engineering background, the first reference I should recommend in the area is the book Applied Statistics and Probability for Engineers by Montgomery & Runger (2003). There, one might find a more detailed description of the fundamentals herein presented and other relevant regression aspects such as multicollinearity, confidence intervals on the mean response, and feature selection.
Those more interested in Machine Learning can refer to The Elements of Statistical Learning by Hastie et al. (2009). In particular, I find it very interesting to see how the authors explain the bias-variance trade-off comparing nearest neighbors to linear models.
Nonlinear regression is also fascinating when one aims to estimate parameters with some fundamental meaning to describe nonlinear phenomena. The book Nonlinear Regression Analysis and Its Applications by Bates & Watts (1988) is a great reference. The subject is also presented in Chapter 3 of the book Generalized Linear Models by Myers et al. (2010).
Lecture notes by professor Cosma Shalizi are available on this link. Currently, the draft is under the title of Advanced Data Analysis from an Elementary Point of View. There, one can find interesting subjects such as Weighting and Variance, Causal Inference, and Dependent Data.
I appreciate the Python package statsmodels. After applying OLS (as we performed in this article), one might be interested in trying WLS for problems with uneven variance of residuals and using VIF for detecting feature multicollinearity.
In this article, the main principles of multiple linear regression were presented, followed by implementation from scratch in Python. The framework was applied to a simple example, in which the statistical significance of parameters was verified besides the main assumptions about residuals in linear least-squares problems. The complete code and additional examples are available in this link.
Bates, D. M. & Watts, D. G., 1988. Nonlinear Regression Analysis and Its Applications. Wiley.
Hastie, T., Tibshirani, R. & Friedman, J. H., 2009. The Elements of Statistical Learning: Data mining, Inference, and Prediction. 2nd ed. New York: Springer.
Montgomery, D. C. & Runger, G., 2003. Applied Statistics and Probability for Engineers. 3rd ed. John Wiley and Sons.
Myers, R. H., Montgomery, D. C., Vining, G. G. & Robinson, T. J., 2012. Generalized linear models: with applications in engineering and the sciences. 2nd ed. Hoboken: John Wiley & Sons.
Shalizi, C., 2021. Advanced Data Analysis from an Elementary Point of View. Cambridge University Press.
